题目内容
5.在等差数列{an}中,首项a1=3,公差d=2,若某学生对其中连续10项迸行求和,在遗漏掉一项的情况下,求得余下9项的和为185,则此连续10项的和为200.分析 先排除不是遗漏掉首项与末项,从而设9项为an,an+1,an+2,…,an+m-1,an+m+1,an+m+2,…,an+9,从而可得10(2n+1)+90-2(m+n)-1=185,从而求得.
解答 解:若遗漏的是10项中的第一项或最后一项,
则185=9•a中,故a中=20$\frac{5}{9}$(舍去);
故设9项为an,an+1,an+2,…,an+m-1,an+m+1,an+m+2,…,an+9,
其中(0<m<9,m∈N*)
故10an+$\frac{10•(10-1)}{2}$×2-am+n=185,
即10(2n+1)+90-2(m+n)-1=185,
故m=9n-43,
故n=5,m=2;
故10×a5+$\frac{10•(10-1)}{2}$×2=110+90=200;
故答案为:200.
点评 本题考查了等差数列的前n项和公式与通项公式的应用.

练习册系列答案
相关题目
20.已知i为虚数单位,复数z=$\frac{a+2i}{1-i}$为纯虚数,则复数|z-1|=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{5}$ | D. | 2 |
10.若图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则这个几何体外接球的表面积为( )
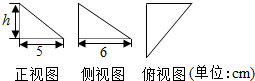

| A. | 25xcm2 | B. | $\frac{77π}{2}$cm2 | C. | 77πcm2 | D. | 144πcm2 |
 如图,在△ABC中,∠C=90°,BC=8,AB=10,O为BC上一点,以O为圆心,OB为半径作半圆与BC边、AB边分别交于点D、E,连结DE.
如图,在△ABC中,∠C=90°,BC=8,AB=10,O为BC上一点,以O为圆心,OB为半径作半圆与BC边、AB边分别交于点D、E,连结DE.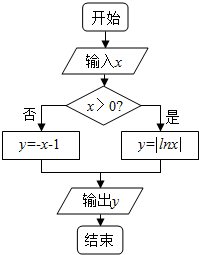 给出如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是2.
给出如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是2.