题目内容
13.为使$\sqrt{cosx}$+lg(4-x2)有意义,x的取值范围是[-$\frac{π}{2}$,$\frac{π}{2}$].分析 根据函数成立的条件建立不等式关系即可得到结论.
解答 解:由$\left\{\begin{array}{l}{cosx≥0}\\{4-{x}^{2}>0}\end{array}\right.$得$\left\{\begin{array}{l}{2kπ-\frac{π}{2}≤x≤2kπ+\frac{π}{2},k∈Z}\\{-2<x<2}\end{array}\right.$,
得-$\frac{π}{2}$≤x≤$\frac{π}{2}$,
故x的取值范围是[-$\frac{π}{2}$,$\frac{π}{2}$],
故答案为:[-$\frac{π}{2}$,$\frac{π}{2}$].
点评 本题主要考查函数定义域的求解,根据函数成立的条件建立不等式关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.如图,已知AB⊥平面BCD,BC⊥CD,M是CD的中点.则二面角A-CD-B的平面角是( )
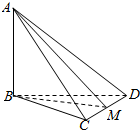

| A. | ∠ADB | B. | ∠BDC | C. | ∠AMB | D. | ∠ACB |
4.已知奇函数y=f(x)的图象关于直线x=-2对称,且f(m)=3,则f(m-4)的值为( )
| A. | 3 | B. | 0 | C. | -3 | D. | $\frac{1}{3}$ |
1.为了考察高中生的性别与是否喜欢数学课程之间的关系,在我市的某校高中生中随即抽取了100名学生,得到如下联表:
由表中数据,计算得K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$≈3.03,
附表:
参照附表,则下列结论正确的是( )
| 不喜欢数学课程 | 喜欢数学课程 | 总计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 总 | 75 | 25 | 100 |
附表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
| A. | 有90%以上的把握认为“性别与是否喜欢数学课程有关” | |
| B. | 有90%以上的把握认为“性别与是否喜欢数学课程没有关” | |
| C. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程有关” | |
| D. | 在犯错误的概率不超过1%的前提下,认为“性别与是否喜欢数学课程没有关” |