题目内容
2．△ABC的内角A，B，C所对的边分别为a，b，c．且a：b：c=3：5：7试判断该三角形的形状（ ）| A． | 钝角三角形 | B． | 锐角三角形 | C． | 直角三角形 | D． | 等边三角形 |
分析 设a=3t，b=5t，c=7t，（t＞0），由余弦定理可求cosC=-$\frac{1}{2}$，可得∠C=120°，即可得解．
解答 解：∵a：b：c=3：5：7，
∴设a=3t，b=5t，c=7t，（t＞0），
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=-$\frac{1}{2}$，
∴∠C=120°，
∴三角形为钝角三角形．
故选：A．
点评 本题考查三角形形状的判定，涉及余弦定理在解三角形中的应用，属基础题．
练习册系列答案
相关题目
7．设（2-x）6=a0+a1（1+x）+a2（1+x）2+…+a6（1+x）6，则a0+a1+a2+a3+a4+a5+a6等于（ ）
| A． | 4 | B． | -71 | C． | 64 | D． | 199 |
14．已知φ∈（$\frac{π}{2}$，π），且sinφ=$\frac{3}{5}$，若函数f（x）=sin（ωx+φ）（ω＞0）的图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$，则f（$\frac{π}{4}$）的值为（ ）
| A． | -$\frac{3}{5}$ | B． | -$\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
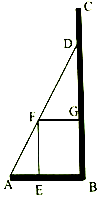如图，为迎接校庆，我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”，规划在△ABD的内接正方形BEFG内种花，其余地方种草，若AB=a，∠DAB=θ，种草的面积为S1，种花的面积为S2，比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”．