题目内容
10.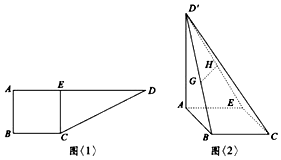 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.(Ⅰ)求证:GH⊥AD';
(Ⅱ)求三棱锥D'-BCE的体积.
分析 (Ⅰ)推导出D′A⊥AE,EC⊥AE,EC⊥D′E,从而EC⊥平面D′AE,进而AB⊥面D′AE,由此得到AB⊥D′A,从而D′A⊥面ABCD,进而D′A⊥BE,由此能证明D′A⊥GH.
(Ⅱ)三棱锥D'-BCE的体积${V}_{{D}^{'}-BCE}$=${V}_{C-{D}^{'}BC}$,由此能求出三棱锥D'-BCE的体积.
解答 证明:(Ⅰ)在△ADE中,∵AD'=2$\sqrt{3}$,D′E=4,AE=2,
∴AD'2+AE2=D′E2,∴D′A⊥AE,
∵EC⊥AE,EC⊥D′E,AE∩D′E=E,
∴EC⊥平面D′AE,
∵AB∥EC,∴AB⊥面D′AE,∴AB⊥D′A,
∵AE∩AB=A,∴D′A⊥面ABCD,
又∵BE?平面ABCD,∴D′A⊥BE,
∵G,H分别为D′B,D′E的中点,连结BE,
∴GH∥BE,∴D′A⊥GH.
解:(Ⅱ)由(Ⅰ)得D′A⊥面ABCD,
∴三棱锥D'-BCE的体积:
${V}_{{D}^{'}-BCE}$=${V}_{C-{D}^{'}BC}$=$\frac{1}{3}×2\sqrt{3}×\frac{1}{2}×2×2$=$\frac{4\sqrt{3}}{3}$.
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、空间思维能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
相关题目
1.若函数f(x)=ln(x2+1)的值域为{0,1,2},从满足条件的所有定义域集合中选出2个集合,则取出的2个集合中各有三个元素的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{9}$ |
18.过圆x2+y2-8x-2y+8=0内一点P(3,-1)的最长弦,最短弦所在的直线方程式分别是( )
| A. | x-y-4=0,2x-y-7=0 | B. | 2x+y-5=0,x-2y-5=0 | ||
| C. | x-2y-1=0,2x-y-7=0 | D. | 2x-y-7=0,x+2y-1=0 |
2.已知曲线$f(x)=\frac{a}{x}(x>0,a>0)$上任一点P(x0,f(x0)),在点P处的切线与x,y轴分别交于A,B两点,若△OAB的面积为4,则实数a的值为( )
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
19.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点(3,2),当a2+b2取得最小值时,椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
20.双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点F到E的渐近线的距离为$\sqrt{3}a$,则E的离心率是( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |