题目内容
设函数f(x)=|x2-4x-5|,当k>6时,求证:在区间[-1,5]上,y=kx+3k的图象位于函数f(x)图象上方.
考点:函数的最值及其几何意义,函数的图象
专题:证明题
分析:首先求出区间[-1,5]上的函数f(x)的解析式,并与直线y=kx+3k联立,消去y,得到关于x的方程,由判别式为0,求出k=2或k=18,结合图象说明k=2相切,k=18无交点,从而说明k>6,结论成立.
解答:
 证明:当x∈[-1,5]时,f(x)=-x2+4x+5,
证明:当x∈[-1,5]时,f(x)=-x2+4x+5,
由
消去y,得x2+(k-4)x+(3k-5)=0
令△=(k-4)2-4(3k-5)=0,
解得 k=2或k=18,
在区间[-1,5]上,
当k=2时,y=2(x+3)的图象与函数f(x)的图象
只交于一点(1,8),
当k=18时,y=18(x+3)的图象与函数f(x)的图象没有交点.
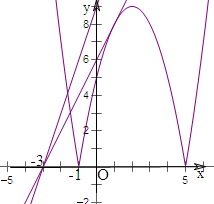
如图可知,由于直线y=k(x+3)过点(-3,0),
当k>6时,直线y=k(x+3)是由直线y=2(x+3)绕点(-3,0)逆时针方向旋转得到.
因此,在区间[-1,5]上,y=kx+3k的图象位于函数f(x)图象的上方.
 证明:当x∈[-1,5]时,f(x)=-x2+4x+5,
证明:当x∈[-1,5]时,f(x)=-x2+4x+5,由
|
消去y,得x2+(k-4)x+(3k-5)=0
令△=(k-4)2-4(3k-5)=0,
解得 k=2或k=18,
在区间[-1,5]上,
当k=2时,y=2(x+3)的图象与函数f(x)的图象
只交于一点(1,8),
当k=18时,y=18(x+3)的图象与函数f(x)的图象没有交点.
如图可知,由于直线y=k(x+3)过点(-3,0),
当k>6时,直线y=k(x+3)是由直线y=2(x+3)绕点(-3,0)逆时针方向旋转得到.
因此,在区间[-1,5]上,y=kx+3k的图象位于函数f(x)图象的上方.
点评:本题主要考查函数图象问题转化为方程有解的问题,结合图象,观察图象的变化,从而得证,这种数形结合的思想在高中数学中应用广泛,值得重视.

练习册系列答案
相关题目
已知数列{an},则“an+1>an-1”是“数列{an}为递增数列”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
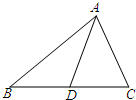 如图,已知△ABC中,∠BAD=30°,∠CAD=45°,AB=3,AC=2,则
如图,已知△ABC中,∠BAD=30°,∠CAD=45°,AB=3,AC=2,则