题目内容
6.已知集合A={(x,y)|$\sqrt{\frac{{x}^{2}}{9}}+\sqrt{\frac{{y}^{2}}{4}}≤1$},B={(x,y)|x-2y≤0},区域M=A∩B,则区域M的面积为( )| A. | 6 | B. | 8 | C. | 12 | D. | 24 |
分析 在数轴上画出集合A中不等式表示区域,由B中不等式得到直线x-2y=0过原点,故区域M的面积为四边形PQRS面积的一半,求出即可.
解答 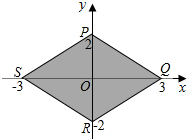 解:集合A中$\sqrt{\frac{{x}^{2}}{9}}$+$\sqrt{\frac{{y}^{2}}{4}}$≤1,等价于$\frac{|x|}{3}$+$\frac{|y|}{2}$≤1,
解:集合A中$\sqrt{\frac{{x}^{2}}{9}}$+$\sqrt{\frac{{y}^{2}}{4}}$≤1,等价于$\frac{|x|}{3}$+$\frac{|y|}{2}$≤1,
当x≥0且y≥0时,$\frac{x}{3}$+$\frac{y}{2}$≤1,再由对称性得到集合A对应的图形,如图所示,
∵直线x-2y=0过原点,
∴区域M的面积S=$\frac{1}{2}$S四边形PQRS=$\frac{1}{2}$×$\frac{1}{2}$×6×4=6,
故选:A.
点评 此题考查了交集及其运算,画出相应的图形是解本题的关键.

练习册系列答案
相关题目
1.设a、b为两条不同的直线,α、β为两个不同的平面,则下列命题中为真命题的是( )
| A. | 若a⊥α,α⊥β,则a∥β | B. | 若a∥α,b∥α,则a∥b | C. | 若a∥α,α⊥β,则a⊥β | D. | 若a⊥α,a∥β,则α⊥β |
18.已知抛物线的方程为y2=8x,过其焦点F的直线l与抛物线交于A、B两点,若S△AOF=S△BOF(O为坐标原点),则|AB|=( )
| A. | $\frac{16}{3}$ | B. | 8 | C. | $\frac{4}{3}$ | D. | 4 |
15.截至11月27日,国内某球员在2015-2016赛季CBA联赛的前10轮比赛中,各场得分xi(i=1,2,3,…,10)的茎叶图如图①所示,图②是该运动员某项成绩指标分析的程序框图,则输出的结果是( )


| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
16.若函数f(x)=kx3+3(k-1)x2+1(k≠0)在区间(0,1)上单调递增,则实数k的取值范围是( )
| A. | k≥1或k≤-$\frac{1}{3}$ | B. | k≤-$\frac{1}{3}$ | C. | k≥$\frac{1}{3}$ | D. | k≥1 |
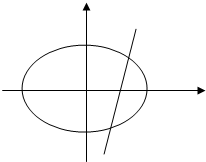 已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.
已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别为F1(-1,0),F2(1,0),且过点$(-1,\frac{3}{2})$,右顶点为A,经过点F2的动直线l与椭圆交于B,C两点.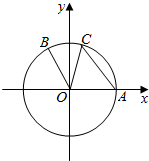 如图,在平面直角坐标系xOy中,以原点为圆心的圆O与x轴的正半轴交于点A,点B(-1,2)在圆O上,点C在弧AB上,且∠BOC为$\frac{π}{4}$.
如图,在平面直角坐标系xOy中,以原点为圆心的圆O与x轴的正半轴交于点A,点B(-1,2)在圆O上,点C在弧AB上,且∠BOC为$\frac{π}{4}$.