题目内容
7.函数y=$\frac{3sinx+1}{3sinx-1}$的值域是(-∞,$-\frac{1}{4}$]∪[$\frac{1}{2}$,+∞).分析 利用分式的性质,结合三角函数的有界性进行求解即可.
解答 解:y=$\frac{3sinx+1}{3sinx-1}$=$\frac{3sinx-1+2}{3sinx-1}$=1+$\frac{2}{3sinx-1}$,
由3sinx-1≠0得sinx≠$\frac{1}{3}$,
∵-1≤sinx≤1且sinx≠$\frac{1}{3}$,
∴-3≤3sinx≤3且3sinx≠1,
∴-4≤3sinx-1≤2且3sinx-1≠0,
即-4≤3sinx-1<0或0<3sinx-1≤2,
则$\frac{1}{3sinx-1}$≤$-\frac{1}{4}$或$\frac{1}{3sinx-1}$≥$\frac{1}{2}$,
即y≤$-\frac{1}{4}$或y≥$\frac{1}{2}$,
即函数的值域为(-∞,$-\frac{1}{4}$]∪[$\frac{1}{2}$,+∞),
故答案为:(-∞,$-\frac{1}{4}$]∪[$\frac{1}{2}$,+∞)
点评 本题主要考查函数值域的求解,利用分式函数的性质利用分子常数化以及利用三角函数的有界性是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知点A(0,1),直线l:y=kx-m与圆O:x2+y2=1交于B,C两点,△ABC和△OBC的面积分别为S1,S2,若∠BAC=60°,且S1=2S2,则实数k的值为±$\sqrt{3}$.
19.若复数z满足(1-i)z=i,则复数z的模为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
16.设集合A={x|x2-2x=0},B={x|x2+2x=0},则A∪B=( )
| A. | {0} | B. | {0,2} | C. | {0,-2} | D. | {2,0,-2} |
17.函数f(x)=2x+3x-7的零点所在的区间是( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
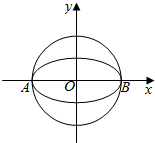 已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
已知椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.