题目内容
10.已知函数f(x)=$\frac{1-x}{ax}$+lnx在(1,+∞)上是增函数,且a>0.(1)求a的取值范围;
(2)求函数g(x)=ln(1+x)-x在[0,+∞)上的最大值.
分析 (1)求出f(x)的导数为${f^'}(x)=-\frac{1}{{a{x^2}}}+\frac{1}{x}$,利用函数f(x)在(1,+∞)上是增函数,${f^'}(x)=-\frac{1}{{a{x^2}}}+\frac{1}{x}≥0$在(1,+∞)上恒成立,得到$x≥\frac{1}{a}$在(1,+∞)上恒成立,然后求解即可;
(2)求出导函数g′(x),判断函数的单调性,然后求解函数的最值.
解答 解:(1)f(x)的导数为${f^'}(x)=-\frac{1}{{a{x^2}}}+\frac{1}{x}$,
因为函数f(x)在(1,+∞)上是增函数,
所以${f^'}(x)=-\frac{1}{{a{x^2}}}+\frac{1}{x}≥0$在(1,+∞)上恒成立,
即$x≥\frac{1}{a}$在(1,+∞)上恒成立,
所以只需$1≥\frac{1}{a}$,
又因为a>0,所以a≥1;
(2)因为x∈[0,+∞),所以${g^'}(x)=\frac{1}{1+x}-1=\frac{-x}{1+x}≤0$
所以g(x)在[0,+∞)上单调递减,
所以g(x)=ln(1+x)-x在[0,+∞)上的最大值为g(0)=0.
点评 本题考查函数的导数的综合应用,函数的极值以及函数的最值的求法,考查计算能力.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
5.已知函数f(x)在点P(1,m)处的切线方程为y=2x-1,函数f(x)的导数为f′(x),则f(1),与f′(1)的大小关系是( )
| A. | f(1)=f′(1) | B. | f(1)>f′(1) | C. | f(1)<f′(1) | D. | 无法判断 |
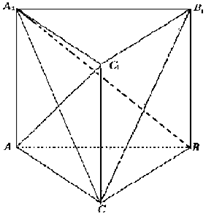 如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=3,BC=4,AB=5,AA1=3
如图,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC=3,BC=4,AB=5,AA1=3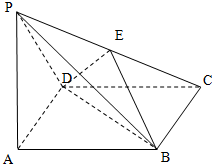 在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,PA=AB,E是PC的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,PA=AB,E是PC的中点.