题目内容
15.已知函数f(x)=lnx+ax2-(2a+1)x,其中a为常数,且a≠0.(1)当a=2时,求f(x)的单调区间;
(2)若f(x)在x=1处取得极值,且在(0,e]的最大值为1,求a的值.
分析 (1)由函数的解析式,可求出函数导函数的解析式,进而根据f′(x)=0,可构造关于a,b的方程,根据a=2求出b值;可得函数导函数的解析式,分析导函数值大于0和小于0时,x的范围,可得函数f(x)的单调区间;
(2)对函数求导,写出函数的导函数等于0的x的值,则f′(1)=0,又由函数在(0,e]上的最大值为1,讨论a,得出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于a的方程求得结果.
解答 解:(1)f(x)=mx=2x2-5x,$f′(x)=\frac{1}{x}+4x-5=\frac{(4x-1)(x-1)}{x}$令f′(x)=0,得x=$\frac{1}{4}$或1,则
| x | (0,$\frac{1}{4}$) | $\frac{1}{4}$ | ($\frac{1}{4},1$) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
(2)∵$f′(x)=\frac{(2ax-1)(x-1)}{x}$,令$f′(x)=0,{x}_{1}=1,{x}_{2}=\frac{1}{2a}$,因为f(x)在x=1处取得极值,
所以x2=$\frac{1}{2a}≠{x}_{1}=1$
①$\frac{1}{2a}<0$时,f(x)在(0,1)上单调递增,在(1,e)上单调递减,所以f(x)在区间(1,e)上的最大值为f(1),令f(1)=1,解得a=-2;
②当a>0,x2=$\frac{1}{2a}>0$;
(i)当$\frac{1}{2a}<1$时,f(x)在(0,$\frac{1}{2a}$)上单调递增,($\frac{1}{2a},1$)上单调递减,(1,e)上单调递增
所以最大值1可能在x=$\frac{1}{2a}$或x=e处取得,
而f($\frac{1}{2a}$)=ln$\frac{1}{2a}$-$\frac{1}{4a}$-1<0,
所以f(e)=lne+ae2-(2a+1)e=1,解得a=$\frac{1}{e-2}$,
(ii)当1≤$\frac{1}{2a}<e$时,f(x)在区间(0,1)上单调递增;(1,$\frac{1}{2a}$)上单调递减,($\frac{1}{2a},e$)上单调递增,所以最大值1可能在x=1或x=e处取得
而f(1)=ln1+a-(2a+1)<0,所以f(e)=lne+ae2-(2a+1)e=1,解得a=$\frac{1}{e-2}$
1<x2=$\frac{1}{2a}<e$矛盾;
(iii)当x2=$\frac{1}{2a}≥e$时,f(X)在区间(0,1)上单调递增,在(1,e)单调递减,
所以最大值1可能在x=1处取得,而f(1)=ln1+a-(2a+1)<0,矛盾,
综上所述,a=$\frac{1}{e-2}$或a=-2.
点评 本题考查的知识点是利用导数研究函数的极值,利用导数研究函数的单调性,以及利用导数研究函数在闭区间上的最值,其中根据已知条件确定a,b值,得到函数导函数的解析式并对其符号进行分析,是解答的关键.属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
4.已知O为△ABC的外心,AB=3,AC=4,$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,且2x+y=1(x,y≠0),则cos∠BAC=( )
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
5.已知函数f(x)=x+$\frac{1}{x}$,下列结论正确的是( )
| A. | x=-1是f(x)的极小值点 | B. | x=1是f(x)的极大值点 | ||
| C. | (1,+∞)是f(x)的单调增区间 | D. | (-1,1)是f(x)的单调增区间 |
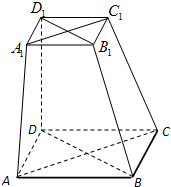 如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.
如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.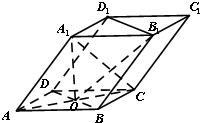 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.