题目内容
函数f(x)=x2-2tx-4(t∈R)在闭区间[0,1]上的最小值记为g(t).则g(t)的函数解析式( )
A、g(t)=
| ||||||
| B、g(t)=-t2+2 | ||||||
| C、g(t)=-t2+2t | ||||||
| D、g(t)=-t2+2t+2 |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:求出对称轴x=t.分类讨论,得出当t≤0时,g(t)=g(0)
当t>1时,g(t)=g(1)
当0<t≤1时,g(t)=g(t)
当t>1时,g(t)=g(1)
当0<t≤1时,g(t)=g(t)
解答:
解:∵函数f(x)=x2-2tx-4(t∈R)在闭区间[0,1]上的最小值记为g(t).
∴当t≤0时,g(t)=g(0)=-4,
当t>1时,g(t)=g(1)=-3-2t,
当0<t≤1时,g(t)=g(t)=-t2-4,
综上:g(t)=-4
故选:A
∴当t≤0时,g(t)=g(0)=-4,
当t>1时,g(t)=g(1)=-3-2t,
当0<t≤1时,g(t)=g(t)=-t2-4,
综上:g(t)=-4
|
故选:A
点评:本题考查了二次函数的闭区间上的最值问题,属于中档题,关键是分类讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列四个函数:①y=x+1;②y=x-1;③y=x2-1;④y=
,其中定义域与值域相同的是( )
| 1 |
| x |
| A、①②③ | B、①②④ |
| C、②③ | D、②③④ |
若椭圆的中心及两个焦点将两条准线之间的距离四等分,则椭圆的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若直线l1,l2的方向向量分别为
=(1,2,3),
=(-
,-1,-
),则l1,l2的位置关系是( )
| v1 |
| v2 |
| 1 |
| 2 |
| 3 |
| 2 |
| A、垂直 | B、重合 |
| C、平行 | D、平行或重合 |

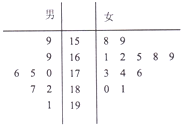 第117届中国进出口商品交易会(简称2015年春季交广会)将于2015年4月15日在广州市举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如茎叶图(单位:m),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.
第117届中国进出口商品交易会(简称2015年春季交广会)将于2015年4月15日在广州市举行,为了搞好接待工作,组委会在广州某大学分别招募8名男志愿者和12名女志愿者,现将这20名志愿者的身高组成如茎叶图(单位:m),若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”.