题目内容
在△ABC中，边a，b，c的对角分别为A，B，C，若a2=b2+c2+
bc，则A的大小为（ ）
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
考点：余弦定理
专题：解三角形
分析：利用余弦定理表示出cosA，将已知等式变形后代入求出cosA的值，即可确定出A的度数．
解答：
解：∵a2=b2+c2+
bc，
即b2+c2-a2=-
bc，
∴cosA=
=-
，
∵A为三角形内角，
∴A=150°．
故选：D．
| 3 |
即b2+c2-a2=-
| 3 |
∴cosA=
| b2+c2-a2 |
| 2bc |
| ||
| 2 |
∵A为三角形内角，
∴A=150°．
故选：D．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
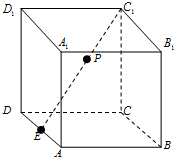如图，长方体ABCD-A1B1C1D1中，AB=3，BC=2，BB1=4，E为AD的中点，点P在线段C1E上，则点P到直线BB1的距离的最小值为（ ）| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
b=0是函数f（x）=x2+bx+c为偶函数的（ ）条件．
| A、充分而不必要 |
| B、必要而不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
已知命题p：?x∈R，使得x+
＜2，命题q：?x∈R，x2+x+1＞0，下列命题为真的是（ ）
| 1 |
| x |
| A、p∧q |
| B、（￢p）∧q |
| C、p∧（￢q） |
| D、（￢p）∧（￢q） |
曲线f（x）=ex-2x+1在点（0，f（0））处的切线方程为x+ay-b=0，则a+b等于（ ）
| A、-l | B、1 | C、-3 | D、3 |
直线L1过点A（m，1）和点B（-1，m），直线L2过点C（m+n，n+1）和点D（n+1，n-m）．则直线L1与L2的位置关系是（ ）
| A、重合 | B、平行 |
| C、垂直 | D、无法确定 |
运行如方框内的程序，若输入x=4，则输出的结果是（ ）| A、12 | B、3 | C、4 | D、5 |