题目内容
已知a=log45,b=4-
,c=sin2,则a、b、c的大小关系是( )
| 1 |
| 2 |
| A、b<c<a |
| B、c<a<b |
| C、a<b<c |
| D、c<b<a |
考点:对数值大小的比较
专题:函数的性质及应用
分析:由对数性质知a=log45>1,由指数性质知b=4-
=
,由三角函数性质知c=sin2>sin
,由此能求出a、b、c的大小关系.
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
解答:
解:∵a=log45>log44=1,
b=4-
=
=
,
1>c=sin2>sin
=
,
∴b<c<a.
故选:A.
b=4-
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| 2 |
1>c=sin2>sin
| π |
| 3 |
| ||
| 2 |
∴b<c<a.
故选:A.
点评:本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意对数、指数、三角函数的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若对数函数y=logax在(0,+∞)上是减函数,那么( )
| A、0<a<1 | B、-1<a<0 |
| C、a=-1 | D、a<-1 |
已知函数y=f(x)(x∈R),g(x)=f(x)+2x(x∈R),则函数f(x)在R上递增是g(x)在R上递增的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
若抛物线x2=2py的焦点为F(0,2),则p的值为( )
| A、-2 | B、2 | C、-4 | D、4 |
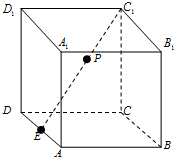 如图,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=4,E为AD的中点,点P在线段C1E上,则点P到直线BB1的距离的最小值为( )
如图,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=4,E为AD的中点,点P在线段C1E上,则点P到直线BB1的距离的最小值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
直线L1过点A(m,1)和点B(-1,m),直线L2过点C(m+n,n+1)和点D(n+1,n-m).则直线L1与L2的位置关系是( )
| A、重合 | B、平行 |
| C、垂直 | D、无法确定 |