题目内容
椭圆
+
=1上有不关于x轴对称的两点P,Q,椭圆焦点为F1,F2,O为原点,N为PQ中点,若kOP•kOQ=-
,则kNF1•kNF2的值为( )
| x2 |
| 4 |
| y2 |
| 2 |
| 1 |
| 2 |
A、-
| ||
B、
| ||
| C、-2 | ||
| D、不确定 |
考点:椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:设P(x1,y1),Q(x2,y2),N(x,y),则x=
,y=
.利用kOP•kOQ=-
,可得
•
=-
,进而表示出kNF1•kNF2,化简可得结论.
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 1 |
| 2 |
| y1 |
| x1 |
| y2 |
| x2 |
| 1 |
| 2 |
解答:
解:设P(x1,y1),Q(x2,y2),N(x,y),则x=
,y=
.
∵椭圆
+
=1,
∴F1(-
,0),F2(
,0),
∵kOP•kOQ=-
,
∴
•
=-
,
∴y1y2=-
x1x2,
∵
+
=1,
+
=1
∴y12+y22=4-
,
∴kNF1•kNF2=
•
=
=
=
=-
.
故选:A.
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
∵椭圆
| x2 |
| 4 |
| y2 |
| 2 |
∴F1(-
| 2 |
| 2 |
∵kOP•kOQ=-
| 1 |
| 2 |
∴
| y1 |
| x1 |
| y2 |
| x2 |
| 1 |
| 2 |
∴y1y2=-
| 1 |
| 2 |
∵
| x12 |
| 4 |
| y12 |
| 2 |
| x22 |
| 4 |
| y22 |
| 2 |
∴y12+y22=4-
| x12+x22 |
| 2 |
∴kNF1•kNF2=
| y | ||
x+
|
| y | ||
x-
|
| y2 |
| x2-2 |
| (y12+y2)2 |
| (x1+x2)2-8 |
4-
| ||
| (x1+x2)2-8 |
| 1 |
| 2 |
故选:A.
点评:本题考查椭圆的几何性质,考查斜率的计算,考查学生的计算能力,正确计算斜率是关键.

练习册系列答案
相关题目
已知函数y=f(x)(x∈R),g(x)=f(x)+2x(x∈R),则函数f(x)在R上递增是g(x)在R上递增的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
若抛物线x2=2py的焦点为F(0,2),则p的值为( )
| A、-2 | B、2 | C、-4 | D、4 |
给定命题p:若x∈R,则x+
≥2;题q:若x≥0,则x2≥0.则下列各命题中,假命题的是( )
| 1 |
| x |
| A、p∨q |
| B、(¬p)∨q |
| C、(¬p)∧q |
| D、(¬p)∧(¬q) |
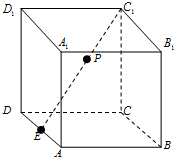 如图,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=4,E为AD的中点,点P在线段C1E上,则点P到直线BB1的距离的最小值为( )
如图,长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=4,E为AD的中点,点P在线段C1E上,则点P到直线BB1的距离的最小值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
b=0是函数f(x)=x2+bx+c为偶函数的( )条件.
| A、充分而不必要 |
| B、必要而不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
 运行如方框内的程序,若输入x=4,则输出的结果是( )
运行如方框内的程序,若输入x=4,则输出的结果是( )| A、12 | B、3 | C、4 | D、5 |