题目内容
新一轮高考改革已经启动,浙江省作为试点省份之一,于2014年9月公布新的高考改革方案,考试科目分为必考科目和选考科目,必考科目为语文、数学和外语,选考科目由学生从思想政治(A)、历史(B)、地理(C)、物理(D)、化学(E)、生物(F)、技术(G)(含通用技术和信息技术)等7门中自主选择3门.
(1)若学生甲已经选定物理、化学2门,第3门再从剩下的选考科目中随机选取,求学生甲选中地理的概率;
(2)若学生乙生物必选,思想政治必不选,其余2门从剩下的选考科目中随机选取,列出所有的基本事件(用科目代号表示),并求地理、化学至少一门被学生乙选中的概率.
(注:题干中字母表示相应的科目代号,如A 为“思想政治”的科目代号)
(1)若学生甲已经选定物理、化学2门,第3门再从剩下的选考科目中随机选取,求学生甲选中地理的概率;
(2)若学生乙生物必选,思想政治必不选,其余2门从剩下的选考科目中随机选取,列出所有的基本事件(用科目代号表示),并求地理、化学至少一门被学生乙选中的概率.
(注:题干中字母表示相应的科目代号,如A 为“思想政治”的科目代号)
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:方法一(1)根据概率公式计算即可.
(2)先一一列举出从剩下的选考科目中随机选取2门的所有基本事件,再找到地理、化学至少一门被学生乙选中的基本事件,根据概率公式计算即可.
方法二(1)根据概率公式计算即可.
(2)先一一列举出从剩下的选考科目中随机选取2门的所有基本事件,再找到地理、化学至少一门被学生乙选中的基本事件的对立事件,根据概率公式计算即可.
(2)先一一列举出从剩下的选考科目中随机选取2门的所有基本事件,再找到地理、化学至少一门被学生乙选中的基本事件,根据概率公式计算即可.
方法二(1)根据概率公式计算即可.
(2)先一一列举出从剩下的选考科目中随机选取2门的所有基本事件,再找到地理、化学至少一门被学生乙选中的基本事件的对立事件,根据概率公式计算即可.
解答:
解:方法一:(1)依题意得,剩下的选考科目共有5门,从中随机选取1门共有5种取法.…(2分)
设“学生甲选中地理”为事件M,则P(M)=
…(6分)
(2)依题意得,从剩下的选考科目中随机选取2门的所有基本事件为:BC,BD,BE,BG,CD,CE,CG,DE,DG,EG共10种 …(9分)
(或FBC,FBD,FBE,FBG,FCD,FCE,FCG,FDE,FDG,FEG)
设“地理、化学至少一门被学生乙选中”为事件N,包括的基本事件为BC,BE,CD,CE,CG,DE,EG共有7种,…(11分)
(或FBC,FBE,FCD,FCE,FCG,FDE,FEG)
所以P(N)=
即地理、化学至少一门被学生乙选中的概率为
.…(13分)
方法二:(1)同方法一;
(2)依题意得,从剩下的选考科目中随机选取2门的所有基本事件为:BC,BD,BE,BG,CD,CE,CG,DE,DG,EG共10种 …(9分)
(或FBC,FBD,FBE,FBG,FCD,FCE,FCG,FDE,FDG,FEG)
设“地理、化学至少一门被学生乙选中”为事件N,则N的对立事件所包含的基本事件有BD,BG,DG共3种.…(11分)
(或FBD,FBG,FDG)
所以P(N)=1-
=
.
即地理、化学至少一门被学生乙选中的概率为
.…(13分)
设“学生甲选中地理”为事件M,则P(M)=
| 1 |
| 5 |
(2)依题意得,从剩下的选考科目中随机选取2门的所有基本事件为:BC,BD,BE,BG,CD,CE,CG,DE,DG,EG共10种 …(9分)
(或FBC,FBD,FBE,FBG,FCD,FCE,FCG,FDE,FDG,FEG)
设“地理、化学至少一门被学生乙选中”为事件N,包括的基本事件为BC,BE,CD,CE,CG,DE,EG共有7种,…(11分)
(或FBC,FBE,FCD,FCE,FCG,FDE,FEG)
所以P(N)=
| 7 |
| 10 |
即地理、化学至少一门被学生乙选中的概率为
| 7 |
| 10 |
方法二:(1)同方法一;
(2)依题意得,从剩下的选考科目中随机选取2门的所有基本事件为:BC,BD,BE,BG,CD,CE,CG,DE,DG,EG共10种 …(9分)
(或FBC,FBD,FBE,FBG,FCD,FCE,FCG,FDE,FDG,FEG)
设“地理、化学至少一门被学生乙选中”为事件N,则N的对立事件所包含的基本事件有BD,BG,DG共3种.…(11分)
(或FBD,FBG,FDG)
所以P(N)=1-
| 3 |
| 10 |
| 7 |
| 10 |
即地理、化学至少一门被学生乙选中的概率为
| 7 |
| 10 |
点评:本题考查了古典概型概率的问题,关键是列举出所有的基本事件,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在三棱锥A-BCD的各边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF∩HG=P,则点P( )
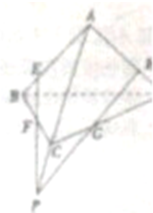

| A、一定在直线BD上 |
| B、一定在直线AC上 |
| C、在直线AC或BD上 |
| D、不在直线AC上,也不在直线BD上 |
设函数f(x)=x2+bx+c,且f(-1)=f(3),则( )
| A、f(-1)<c<f(1) |
| B、c<f(-1)<f(1) |
| C、f(1)<f(-1)<c |
| D、f(1)<c<f(-1) |