题目内容
14.2015年7月31日,国际奥委会在吉隆坡正式宣布2022年奥林匹克冬季运动会(简称冬奥会)在北京和张家口两个城市举办,某中学为了普及奥运知识,举行了一次奥运知识竞赛,分析发现,成绩x服从正态分布,即x~N(85,σ2)(满分100分),已知P(x<80)=0.2,P(x≥95)=0.1,任意选取3名考生.(I)求抽到的3名考生成绩在[80,90)、[90,95)和[95,100]内各有1名考生的概率;
(Ⅱ)记抽到的3名同学中,成绩在[80,90)的人数是ξ,求ξ的分布列和期望.
分析 (1)由已知得P(80≤ξ<90)=1-0.2-0.2=0.6,P(90≤ξ<95)=0.2-0.1=0.1,P(95≤ξ<100)=0.1,由此能求出抽到的三位同学该次体能测试成绩在区间[80,90),[90,95),[95,100]各有一位同学的概率.
(2)由已知得ξ服从二项分布B(3,0.6),由此能求出随机变量ξ的分布列和数学期望Eξ.
解答 解:(Ⅰ)∵P(x<80)=0.2,P(x≥95)=0.1,
∴P(80≤ξ<90)=1-0.2-0.2=0.6,
P(90≤ξ<95)=0.2-0.1=0.1,
P(95≤ξ<100)=0.1,
∴抽到的3名考生成绩在[80,90)、[90,95)和[95,100]内各有1名考生的概率:
p=${A}_{3}^{3}×0.6×0.1×0.1$=0.036.
(Ⅱ)∵抽到的3名同学中,成绩在[80,90)的人数是ξ,P(80≤ξ<90)=0.6,
∴ξ~B(3,0.6),
P(ξ=0)=${C}_{3}^{0}(0.4)^{3}$=0.064,
P(ξ=1)=${C}_{3}^{1}×0.6×(0.4)^{2}$=0.288,
P(ξ=2)=${C}_{3}^{2}×(0.6)^{2}×0.4$=0.432,
P(ξ=3)=${C}_{3}^{3}×(0.6)^{3}$=0.216,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | 0.064 | 0.288 | 0.432 | 0.216 |
点评 本题考查概率的求法,考查离散型随机就是的分布列和数学期望的合理运用,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
5.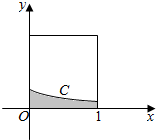 在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )
在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )
附“若X~N(μ,σ2),则
P(μ-σ<X≤μ+σ)=0.6826.
p(μ-2σ<X≤μ+2σ)=0.9544.
 在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )
在如图所示的正方形中随机投掷10000 个点,则落入阴影部分(曲线C为正态分布N(-1,1)的密度曲线)的点的个数的估计值( )附“若X~N(μ,σ2),则
P(μ-σ<X≤μ+σ)=0.6826.
p(μ-2σ<X≤μ+2σ)=0.9544.
| A. | 1193 | B. | 1359 | C. | 2718 | D. | 3413 |
9.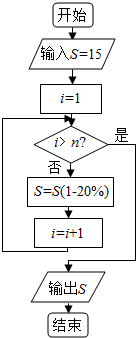 某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )
某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )
 某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )
某人以15万元买了一辆汽车,此汽车将以每年20%的速度折旧,如图是描述汽车价值变化的算法流程图,则当n=4吋,最后输出的S的值为( )| A. | 9.6 | B. | 7.68 | C. | 6.144 | D. | 4.9152 |
19.在如下程序框图中,已知f0(x)=sinx,则输出的结果是( )


| A. | sinx | B. | cosx | C. | -sinx | D. | -cosx |
3.将4名同学录取到3所大学,则每所大学至少录取一名的概率为( )
| A. | $\frac{4}{27}$ | B. | $\frac{8}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{8}{9}$ |
4.在区间[-1,3]内任选一个实数,则x恰好在区间[1,3]内的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |