题目内容
已知关于x的不等式ax2-3x+6>4的解集为(-∞,1)∪(b,+∞).
(1)求a,b的值;
(2)求关于x的不等式cx2-bx+a<0(c<0)的解集;
(3)若关于x的不等式ax2-dx+bd<0的解集中恰有两个整数,求实数d的取值范围.
(1)求a,b的值;
(2)求关于x的不等式cx2-bx+a<0(c<0)的解集;
(3)若关于x的不等式ax2-dx+bd<0的解集中恰有两个整数,求实数d的取值范围.
考点:二次函数的性质
专题:不等式的解法及应用
分析:(1)根据不等式的解集和对应方程之间的关系即可求出a,b的值.
(2)根据不等式的解法解不等式即可.
(3)根据不等式的解集确定条件即可求d的取值范围.
(2)根据不等式的解法解不等式即可.
(3)根据不等式的解集确定条件即可求d的取值范围.
解答:
解:(1)∵不等式ax2-3x+6>4的解集为(-∞,1)∪(b,+∞).
∴x=1或x=b是方程ax2-3x+6=4的两个根,
即a-3+6=4,解得a=1,
此时方程为x2-3x+2=0,解得b=2,
即a=1,b=2.
(2)由(1)知不等式为cx2-2x+1<0(c<0)
∴x2-
x+
>0
∴解为:(-∞,
)∪(
,+∞).
(3)设f(x)=x2-dx+2d,由△>0得d>8或d<0
①当d<0时,f(0)<0且对称轴在y轴的左侧,两整数为0,-1,
∴
,解得-1≤d<-
.
②当d>8时,f(4)<0,且对称轴x=
>4,两整数为4,5
∴
,解得
<d≤9.
综上:-1≤d<-
或
<d≤9.
∴x=1或x=b是方程ax2-3x+6=4的两个根,
即a-3+6=4,解得a=1,
此时方程为x2-3x+2=0,解得b=2,
即a=1,b=2.
(2)由(1)知不等式为cx2-2x+1<0(c<0)
∴x2-
| 2 |
| c |
| 1 |
| c |
∴解为:(-∞,
1+
| ||
| c |
1-
| ||
| c |
(3)设f(x)=x2-dx+2d,由△>0得d>8或d<0
①当d<0时,f(0)<0且对称轴在y轴的左侧,两整数为0,-1,
∴
|
| 1 |
| 3 |
②当d>8时,f(4)<0,且对称轴x=
| d |
| 2 |
∴
|
| 25 |
| 3 |
综上:-1≤d<-
| 1 |
| 3 |
| 25 |
| 3 |
点评:本题主要考查一元二次不等式的解法,要求熟练掌握三个二次之间的关系和相互之间的转化.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
已知非负实数a,b满足a+b≤1,则关于x的一元二次方程x2+ax+b2=0有实根的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是某城市的一个艺术雕塑几何体的三视图,根据图中数据,可得该几何体的表面积是( )


| A、264 | B、228 |
| C、192 | D、156 |
设函数f(x)=x2+
-a(x≠0),a为常数且a>2,则f(x)的零点个数是( )
| 1 |
| x |
| A、1 | B、2 | C、3 | D、4 |
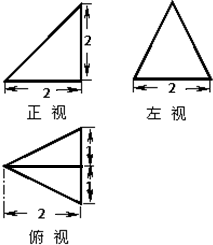 已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),那么可得这个几何体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|