题目内容
若直线y=kx与圆x2+(y-b)2=1的两个交点关于直线3x+y-6=0对称,则
= .
| b |
| k |
考点:直线与圆相交的性质
专题:直线与圆
分析:由题意可得圆心(0,b)在直线3x+y-6=0上,直线y=kx和直线3x+y-6=0垂直,求得b、k的值,可得
的值.
| b |
| k |
解答:
解:直线y=kx与圆x2+(y-b)2=1的两个交点关于直线3x+y-6=0对称,
∴圆心(0,b)在直线3x+y-6=0上,故有0+b-6=0,解得b=6.
再由直线y=kx和直线3x+y-6=0垂直可得 k×(-3)=-1,解得 k=
,∴
=18,
故答案为:18.
∴圆心(0,b)在直线3x+y-6=0上,故有0+b-6=0,解得b=6.
再由直线y=kx和直线3x+y-6=0垂直可得 k×(-3)=-1,解得 k=
| 1 |
| 3 |
| b |
| k |
故答案为:18.
点评:本题主要考查求直线和圆相交的性质,两条直线垂直的性质,体现了转化的数学思想,属于中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
函数f(x)=
+cosx在[0,+∞)内( )
| x |
| A、有无穷多个零点 |
| B、没有零点 |
| C、有且仅有一个零点 |
| D、有且仅有两个零点 |
等差数列{1-3n},公差d=( )
| A、1 | B、3 | C、-3 | D、n |
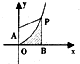 如图,已知点A(0,1),点P(x0,y0)(x0>0)在曲线y=x2上移动,过P点作PB⊥x轴于B,若曲线y=x2在第一象限内把梯形AOBP的面积平分,则P点的坐标为
如图,已知点A(0,1),点P(x0,y0)(x0>0)在曲线y=x2上移动,过P点作PB⊥x轴于B,若曲线y=x2在第一象限内把梯形AOBP的面积平分,则P点的坐标为 如图甲、乙两名同学进入高中以来5次体育测试成绩的茎叶图,则甲5次测试成绩的平均数与乙5次测试成绩的中位数之差是
如图甲、乙两名同学进入高中以来5次体育测试成绩的茎叶图,则甲5次测试成绩的平均数与乙5次测试成绩的中位数之差是 如图中的程序框图所描述的算法为欧几里得辗转相除法,若输入m=11077,n=2014,则输出m=
如图中的程序框图所描述的算法为欧几里得辗转相除法,若输入m=11077,n=2014,则输出m=