题目内容
1.中心在原点,焦点在y轴上,虚轴长为$4\sqrt{2}$并且离心率为3的双曲线的渐近线方程为y=±$\frac{\sqrt{2}}{4}$x.分析 设双曲线的方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a,b>0),由题意可得b,运用离心率公式和a,b,c的关系,可得a=1,可得双曲线的方程,即可得到渐近线方程.
解答 解:设双曲线的方程为$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a,b>0),
由题意可得2b=4$\sqrt{2}$,即b=2$\sqrt{2}$,
又e=$\frac{c}{a}$=3,c2=a2+b2,
解得a=1,
可得双曲线的方程为y2-$\frac{{x}^{2}}{8}$=1,
即有渐近线的方程为y=±$\frac{\sqrt{2}}{4}$x.
故答案为:y=±$\frac{\sqrt{2}}{4}$x.
点评 本题考查双曲线的渐近线方程的求法,注意运用离心率公式和基本量的关系,考查运算能力,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.角α的终边上一点的坐标为$(2sin\frac{2π}{3},2cos\frac{2π}{3})$,则sinα等于( )
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{2}$ |
16. 如图,在四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AC与BD相交于点O,点P是侧棱SC上一动点,则一定与平面PBD垂直的平面是( )
如图,在四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AC与BD相交于点O,点P是侧棱SC上一动点,则一定与平面PBD垂直的平面是( )
 如图,在四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AC与BD相交于点O,点P是侧棱SC上一动点,则一定与平面PBD垂直的平面是( )
如图,在四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AC与BD相交于点O,点P是侧棱SC上一动点,则一定与平面PBD垂直的平面是( )| A. | 平面SAB | B. | 平面SAC | C. | 平面SCD | D. | 平面ABCD |
6.双曲线$\frac{x^2}{{{m^2}+5}}-\frac{y^2}{{4-{m^2}}}$=1的焦距是( )
| A. | 4 | B. | 2$\sqrt{5}$ | C. | 6 | D. | 与m有关 |
10.已知双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右顶点为A,B,点M在E上,△ABM为等腰三角形,且顶角θ满足cosθ=-$\frac{1}{3}$,则E的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
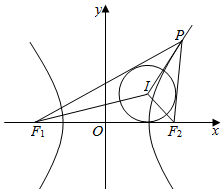 已知点P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上一点,F1,F2分别为双曲线的左右焦点,且|F1F2|=$\frac{{b}^{2}}{a}$,I为△PF1F2的内心,若λS${\;}_{△IP{F}_{1}}$=λS${\;}_{△IP{F}_{2}}$+S${\;}_{△I{F}_{1}{F}_{2}}$成立,则λ的值为$\sqrt{2}$-1.
已知点P为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上一点,F1,F2分别为双曲线的左右焦点,且|F1F2|=$\frac{{b}^{2}}{a}$,I为△PF1F2的内心,若λS${\;}_{△IP{F}_{1}}$=λS${\;}_{△IP{F}_{2}}$+S${\;}_{△I{F}_{1}{F}_{2}}$成立,则λ的值为$\sqrt{2}$-1.