题目内容
已知函数f(x)=
cos(2x-φ)的图象过点(
,
),
①求φ的值;
②将函数y=f(x)的图象上各点的横坐标缩短到原来的
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在(0,
)上的最大值和最小值.
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
①求φ的值;
②将函数y=f(x)的图象上各点的横坐标缩短到原来的
| 1 |
| 2 |
| π |
| 4 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:①直接把点(
,
)代入函数解析式,即可求得φ值;
②利用三角函数图象的平移得到函数y=g(x)的解析式,然后根据x的范围求得函数y=g(x)在(0,
)上的最大值和最小值.
| π |
| 6 |
| 1 |
| 2 |
②利用三角函数图象的平移得到函数y=g(x)的解析式,然后根据x的范围求得函数y=g(x)在(0,
| π |
| 4 |
解答:
解:①∵函数f(x)=
cos(2x-φ)的图象过点(
,
),
∴
cos(2×
-φ)=
,即cos(
-φ)=1,
∴
-φ=2kπ,k∈Z.
则φ=2kπ+
,k∈Z;
②函数f(x)=
cos(2x-2kπ-
)=
cos(2x-
),
将函数y=f(x)的图象上各点的横坐标缩短到原来的
,纵坐标不变,得到函数y=g(x)的图象,
则对应图象的函数解析式为g(x)=
cos(4x-
),
由x∈(0,
),得4x-
∈(-
,
),
∴
cos(4x-
)∈(-
,
].
∴函数y=g(x)在(0,
)上的最大值为
,无最小值.
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
∴
| π |
| 3 |
则φ=2kπ+
| π |
| 3 |
②函数f(x)=
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
将函数y=f(x)的图象上各点的横坐标缩短到原来的
| 1 |
| 2 |
则对应图象的函数解析式为g(x)=
| 1 |
| 2 |
| π |
| 3 |
由x∈(0,
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
∴函数y=g(x)在(0,
| π |
| 4 |
| 1 |
| 2 |
点评:本题考查了由y=Asin(ωx+φ)的部分图象求函数解析式,考查了三角函数值域的求法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
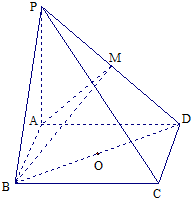 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以BD的中点O为球心、BD为直径的球面交PD于点M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以BD的中点O为球心、BD为直径的球面交PD于点M.