Question

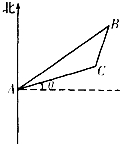如图所示，位于东海某岛的雷达观测站A，发现其北偏东45°，与观测站A距离20

2

海里的B处有一货船正匀速直线行驶，半小时后，又测得该货船位于观测站A东偏北θ（0°＜θ＜45°）的C处，且cosθ=

4

5

，已知A、C两处的距离为10海里，则该货船的船速为

 

海里/小时．

Answer 1

考点：解三角形的实际应用

专题：解三角形

分析：根据余弦定理求出BC的长度即可得到结论．

解答： 解：∵cosθ=

4

5

，∴sin=

3

5

，
由题意得∠BAC=45°-θ，即cos∠BAC=cos（45°-θ）=

2

2

(

4

5

+

3

5

)=

7 2

10

，
∵AB=20

2

，AC=10，
∴由余弦定理得BC²=AB²+AC²-2AB•ACcos∠BAC，
即BC²=（20

2

）²+10²-2×20

2

×10×

7 2

10

=800+100-560=340，
即BC=

340

=2

85

，
设船速为x，则

1

2

x=2

85

，
∴x=4

85

（海里/小时），
故答案为：4

85

点评：本题主要考查解三角形的应用，根据条件求出cos∠BAC，以及利用余弦定理求出BC的长度是解决本题的关键．