题目内容
已知函数f(x)=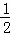 ax2﹣(2a+1)x+2lnx(a>0).
ax2﹣(2a+1)x+2lnx(a>0).
(Ⅰ) 若a≠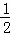 ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(Ⅱ)当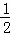 <a<1时,判断函数f(x)在区间[1,2]上有无零点?写出推理过程.
<a<1时,判断函数f(x)在区间[1,2]上有无零点?写出推理过程.
【解析】(Ⅰ)∵ (x>0).
(x>0).
即  (x>0).
(x>0).
∵ ,∵
,∵
∴ 时,
时,
 时,
时, ,由f'(x)>0得
,由f'(x)>0得 或x<2
或x<2
由f'(x)<0得
所以当 ,f(x)的单调递增区间是(0,2]和
,f(x)的单调递增区间是(0,2]和 ,单调递减区间是
,单调递减区间是
同理当 ,f(x)的单调递增区间是
,f(x)的单调递增区间是 和[2,+∞),单调递减区间是
和[2,+∞),单调递减区间是
(Ⅱ)由(Ⅰ)可知,
当 时,f(x)在
时,f(x)在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
故 .
.
由 可知﹣2﹣2lna<0,f(x)max<0,
可知﹣2﹣2lna<0,f(x)max<0,
故在区间[1,2]f(x)<0.恒成立.
故当 时,函数f(x)在区间[1,2]上没有零点.
时,函数f(x)在区间[1,2]上没有零点.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
某品牌汽车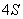 店对最近
店对最近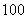 位采用分期付款的购车者进行统计,统计结果如下表示所示:
位采用分期付款的购车者进行统计,统计结果如下表示所示:
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 |
| 10 |
|
已知分3期付款的频率为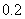 ,
,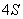 店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为
店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为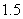 万元;分4期或5期付款,其利润为
万元;分4期或5期付款,其利润为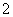 万元,用
万元,用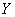 表示经销一辆汽车的利润。
表示经销一辆汽车的利润。
(1)求上表中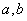 的值;
的值;
(2)若以频率作为概率,求事件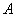 :“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率
:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率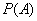 ;
;
(3)求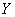 的分布列及数学期望
的分布列及数学期望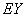 。
。
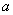

 的最大值是 _________ .
的最大值是 _________ . 的焦点F与双曲
的焦点F与双曲 的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且
的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且 ,则A点的横坐标为
,则A点的横坐标为 (B)3 (C)
(B)3 (C) (D)4
(D)4 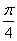 ,
,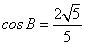 .
.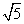 ,D为AB的中点,求CD的长.
,D为AB的中点,求CD的长. :
: ,
, :
: .若
.若 .
. :
:
 与直线
与直线 相交于点
相交于点 ,则
,则 的值为 .
的值为 . 的定义域为 .
的定义域为 . 中,直线
中,直线 的参数方程为
的参数方程为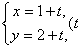 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点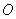 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,圆
轴的正半轴为极轴的极坐标系下,圆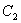 的方程为
的方程为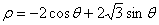 .
.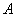 、
、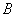 ,求弦
,求弦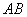 的长.
的长.