题目内容
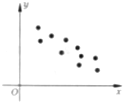 设(x1,y1),(x2,y2),…(xn,yn)是变量x,和y的n个样本点,直线l是由这样样本点通过最小二乘法得到的线性回归方程(如图),则下列结论中正确的是( )
设(x1,y1),(x2,y2),…(xn,yn)是变量x,和y的n个样本点,直线l是由这样样本点通过最小二乘法得到的线性回归方程(如图),则下列结论中正确的是( )| A、x和y正相关 |
| B、x和y的相关系数为直线l的斜率 |
| C、当n为偶数时,分布在l两侧的样本点的个数一定相同 |
| D、x和y的相关系数在-1到0之间 |
考点:散点图
专题:概率与统计
分析:根据散点图的特征以及变量x,y之间的相关系,对四个选项进行分析即可.
解答:
解:对于A,由散点图知,随着x的增加,y逐渐减少,∴x和y是负相关,∴A错误;
对于B,x和y的相关系数和直线的斜率存在一定的关系,但并不是直线l的斜率,∴B错误;
对于C,当n为偶数时,分布在l两侧的样本点的个数没有直接的关系,∴C错误;
对于D,由散点图的分布可以得出x和y的相关系数在-1到0之间,∴D正确.
故选:D.
对于B,x和y的相关系数和直线的斜率存在一定的关系,但并不是直线l的斜率,∴B错误;
对于C,当n为偶数时,分布在l两侧的样本点的个数没有直接的关系,∴C错误;
对于D,由散点图的分布可以得出x和y的相关系数在-1到0之间,∴D正确.
故选:D.
点评:本题考查了根据散点图判断两个变量之间的相关关系的应用问题,是基础题目.

练习册系列答案
相关题目
过双曲线
-
=1(a>0,b>0)的左焦点F1,作圆x2+y2=a2的切线交双曲线右支于点P,切点为T,PF1的中点M在第一象限,则以下结论正确的是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、b-a=|MO|-|MT| |
| B、b-a>|MO|-|MT| |
| C、b-a<|MO|-|MT| |
| D、b-a=|MO|+|MT| |
已知随机变量ξ服从正态分布N(1,σ2),若p(ξ>2)=0.16,则p{0<ξ<1}=( )
| A、0.68 | B、0.32 |
| C、0.42 | D、0.34 |
若执行如图的程序框图,输出S的值为4,则判断框中应填入的条件是( )
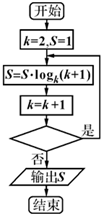

| A、k<14? |
| B、k<15? |
| C、k<16? |
| D、k<17? |
将函数y=sin(2x+ϕ)的图象沿x轴向左平移
个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为( )
| π |
| 8 |
A、
| ||
B、
| ||
| C、0 | ||
D、-
|