题目内容
已知抛物线C:y2=ax与双曲线
-
=1的右焦点重合.
(1)求抛物线C的方程;
(2)过点A(2.0)作倾斜角为
的直角,与抛物线C交于M、N两点,判断∠MON是否为直角.若角MON为直角,请给出证明:若不是直角,请说明理由.
| x2 |
| 2 |
| y2 |
| 2 |
(1)求抛物线C的方程;
(2)过点A(2.0)作倾斜角为
| π |
| 4 |
考点:直线与圆锥曲线的关系,抛物线的标准方程,双曲线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)确定双曲线
-
=1的右焦点为(2,0),可得
=2,即可求抛物线C的方程;
(2)由题意得直线方程为y=x-2,与抛物线方程联立,证明x1x2+y1y2=4-16≠0,即可得出结论.
| x2 |
| 2 |
| y2 |
| 2 |
| a |
| 4 |
(2)由题意得直线方程为y=x-2,与抛物线方程联立,证明x1x2+y1y2=4-16≠0,即可得出结论.
解答:
解:(1)双曲线
-
=1的右焦点为(2,0),故
=2,解得a=8.
∴所求抛物线方程为y2=8x;
(2)由题意得直线方程为y=x-2,设交点坐标为M(x1,y1),N(x2,y2),
联立方程组
,可化为x2-12x+4=0,△>0
∴x1+x2=12,x1x2=4,
∴y1y2=(x1-2)(x2-2)=-16,
故x1x2+y1y2=4-16≠0,
∴OM、ON不垂直,即∠MON不是直角.
| x2 |
| 2 |
| y2 |
| 2 |
| a |
| 4 |
∴所求抛物线方程为y2=8x;
(2)由题意得直线方程为y=x-2,设交点坐标为M(x1,y1),N(x2,y2),
联立方程组
|
∴x1+x2=12,x1x2=4,
∴y1y2=(x1-2)(x2-2)=-16,
故x1x2+y1y2=4-16≠0,
∴OM、ON不垂直,即∠MON不是直角.
点评:本题考查双曲线的几何性质,考查抛物线的方程,考查直线与抛物线的位置关系,考查韦达定理的运用,确定抛物线方程是关键.

练习册系列答案
相关题目
已知角α的终边经过点(12,-5),则sinα等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
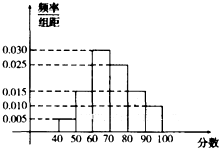 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生500名,据此估计,该模块测试成绩不少于60分的学生人数为
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生500名,据此估计,该模块测试成绩不少于60分的学生人数为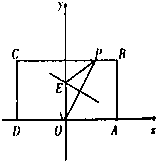 如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足
如图,在矩形ABCD中,已知A(2,0),C(-2,2),点P在BC边上移动,线段OP的垂直平分线交y轴于点E,点M满足