题目内容
已知双曲线
-
=1（a＞0，b＞0）的左右焦点分别为F1、F2，P为右支上一点，点Q满足
=λ1
（λ1＞0）且|
|=2a，双曲线上的点T满足：
=λ2
，
•
=0，则|OT|的值为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| F1Q |
| QP |
| F1Q |
| F2T |
| TQ |
| PT |
| F2Q |
| A、4a | ||
| B、2a | ||
| C、a | ||
D、
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线的定义，结合题意|
|=2a证出
=
，即△PQF2是等腰三角形．由
•
=0得
⊥
，
所以PT是等腰△PQF2底边上的中线，从而证出OT是△QF1F2的中位线，可得|OT|的值为a．
| F1Q |
| |PQ| |
| |PF2| |
| PT |
| F2Q |
| PT |
| F2Q |
所以PT是等腰△PQF2底边上的中线，从而证出OT是△QF1F2的中位线，可得|OT|的值为a．
解答：
解：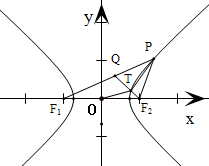
∵点P在双曲线
-
=1的右支上，
∴根据双曲线的定义，可得
-
=2a，
又∵|
|=2a，可得
-
=2a，
∴
=
，即△PQF2是等腰三角形．
∵
•
=0，可得
⊥
，
∴PT是等腰△PQF2底边上的中线，
因此△QF1F2中，OT是中位线，可得|OT|=
|F1Q|=a．
故选：C
∵点P在双曲线| x2 |
| a2 |
| y2 |
| b2 |
∴根据双曲线的定义，可得
| |PF1| |
| |PF2| |
又∵|
| F1Q |
| |PF1| |
| |PQ| |
∴
| |PQ| |
| |PF2| |
∵
| PT |
| F2Q |
| PT |
| F2Q |
∴PT是等腰△PQF2底边上的中线，
因此△QF1F2中，OT是中位线，可得|OT|=
| 1 |
| 2 |
故选：C
点评：本题给出双曲线满足的条件，求线段OT的长．着重考查了双曲线的定义及简单几何性质、向量的数量积运算性质等知识，属于中档题．
练习册系列答案
相关题目
若α∈（
，π），则3cos2α=sin（
-α），则sin2α的值为（ ）
| π |
| 2 |
| π |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知△ABC中，a=2，sinA：sinB=
：3，则边b=（ ）
| 3 |
A、
| ||
B、2
| ||
C、3
| ||
| D、3 |
各项均为正数的等比数列{an}中，2a1+a2=a3，则
的值为（ ）
| a4+a5 |
| a3+a4 |
| A、-1 | B、-1或2 | C、3 | D、2 |
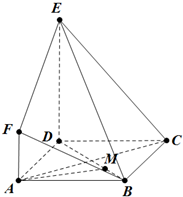如图，ABCD是边长为2的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF=3．
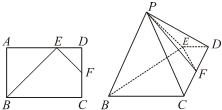如图，在矩形ABCD中，点E为边AD上的点，点F为边CD的中点，AB=AE=