题目内容
f(x)=
,则f(0)+f(
)+f(
)+…+f(
)+f(1)= .
| 4x |
| 4x+2 |
| 1 |
| 10 |
| 2 |
| 10 |
| 9 |
| 10 |
考点:函数的值
专题:函数的性质及应用
分析:由已知得f(x)+f(1-x)=1,由此能求出f(0)+f(
)+f(
)+…+f(
)+f(1)的值.
| 1 |
| 10 |
| 2 |
| 10 |
| 9 |
| 10 |
解答:
解:∵f(x)=
,
∴f(x)+f(1-x)=
+
=
+
=1,
∴f(0)+f(
)+f(
)+…+f(
)+f(1)
=5×1+f(
)
=5+
=5+
=
.
故答案为:
.
| 4x |
| 4x+2 |
∴f(x)+f(1-x)=
| 4x |
| 4x+2 |
| 41-x |
| 41-x+2 |
| 4x |
| 4x+2 |
| 2 |
| 4x+2 |
∴f(0)+f(
| 1 |
| 10 |
| 2 |
| 10 |
| 9 |
| 10 |
=5×1+f(
| 1 |
| 2 |
=5+
4
| ||
4
|
=5+
| 1 |
| 2 |
=
| 11 |
| 2 |
故答案为:
| 11 |
| 2 |
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
下列函数中,是奇函数的是( )
| A、y=x2+x |
| B、y=x2+1 |
| C、y=x3+x |
| D、y=x2+x3 |
经过点P(0,1),Q(2,1)的直线在y轴上的截距为( )
| A、-1 | B、1 | C、-2 | D、2 |
为了调查任教班级的作业完成的情况,将班级里的52名学生随机编号,用系统抽样的方法抽取一个容量为4的样本,已知5号、31号、44号同学在样本中,那么样本中还有一位同学的编号应该是( )
| A、13 | B、17 | C、18 | D、21 |
把二进制数110011(2)化为十进制数( )
| A、48 | B、49 | C、50 | D、51 |
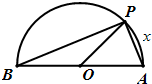 如图,点P在半径为1的半圆上运动,AB是直径,当P沿半圆弧从A到B运动时,点P经过的路程x与△APB的面积y的函数y=f(x)的图象是下图中的( )
如图,点P在半径为1的半圆上运动,AB是直径,当P沿半圆弧从A到B运动时,点P经过的路程x与△APB的面积y的函数y=f(x)的图象是下图中的( )