题目内容
经过点P(0,1),Q(2,1)的直线在y轴上的截距为( )
| A、-1 | B、1 | C、-2 | D、2 |
考点:直线的两点式方程
专题:直线与圆
分析:由题意可得过点P(0,1),Q(2,1)的直线方程为y=1.则直线在y轴上的截距可求.
解答:
解:∵直线过点P(0,1),Q(2,1),
则直线方程为y=1,
∴直线在y轴上的截距为1.
故选:B.
则直线方程为y=1,
∴直线在y轴上的截距为1.
故选:B.
点评:本题考查了直线方程的两点式,考查了直线在y轴上的截距,是基础题.

练习册系列答案
相关题目
由下列各组命题构成“p或q”“p且q”“非p”形式的命题中,“p或q”为真,“p且q”为假,“非p”为真的是( )
| A、p:3是偶数;q:4是奇数 | ||
| B、p:3+2=6;q:5>3 | ||
| C、p:a∈{a,b};q:{a}⊆{a,b} | ||
D、p:y2=x的焦点到准线的距离为
|
设集合U={1,2,3,4,5,6},A={1,2,3},B={2,5},则(∁UA)∩(∁UB)=( )
| A、{2,3,6} |
| B、{4,6} |
| C、{3,6} |
| D、{5,6} |
已知2弧度的圆心角在某扇形中所对弦长为2,则在此扇形中它所对的弧长为( )
| A、2 | ||
| B、sin2 | ||
C、
| ||
| D、2sin1 |
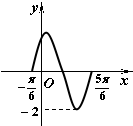
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则( )

A、y=2sin(2x+
| ||
B、y=2sin(2x-
| ||
C、y=2sin(x+
| ||
D、y=-2sin(x+
|