题目内容
已知定点A(0,-1),点B在圆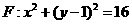 上运动,
上运动,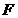 为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹
为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹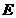 的方程;若曲线
的方程;若曲线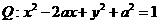 被轨迹
被轨迹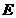 包围着,求实数
包围着,求实数 的最小值.(2)已知
的最小值.(2)已知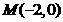 、
、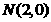 ,动点
,动点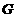 在圆
在圆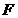 内,且满足
内,且满足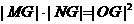 ,求
,求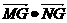 的取值范围.
的取值范围.
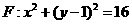 上运动,
上运动,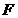 为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹
为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹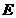 的方程;若曲线
的方程;若曲线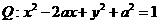 被轨迹
被轨迹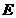 包围着,求实数
包围着,求实数 的最小值.(2)已知
的最小值.(2)已知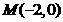 、
、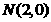 ,动点
,动点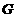 在圆
在圆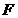 内,且满足
内,且满足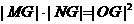 ,求
,求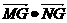 的取值范围.
的取值范围. (1)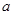 的最小值为
的最小值为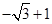 (2)
(2) 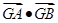 的取值范围为
的取值范围为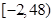
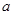 的最小值为
的最小值为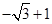 (2)
(2) 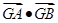 的取值范围为
的取值范围为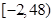
本试题主要是考查了椭圆方程的求解借助于椭圆的定义得到结论。然后结合向量的关系式得到坐标关系,然后利用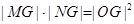 ,得到范围。
,得到范围。
(1)由题意得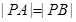 ,∴
,∴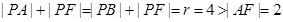
∴P点轨迹是以A、F为焦点的椭圆,进而得到结论。而曲线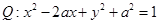 化为
化为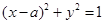 ,
,
则曲线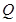 是圆心在
是圆心在 ,半径为1的圆。
,半径为1的圆。
,那么利用图像法得到最值。
(2)设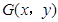 ,由
,由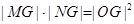 得:
得: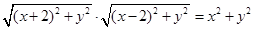 ,
,
化简得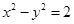 ,即
,即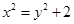 ,
,
而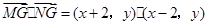
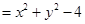
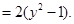
∵点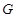 在圆
在圆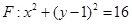 内,∴
内,∴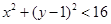 ,得到不等式,然后求解得到。
,得到不等式,然后求解得到。
解:(1)由题意得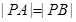 ,∴
,∴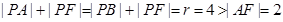
∴P点轨迹是以A、F为焦点的椭圆. ………………………3分
设椭圆方程为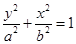
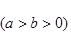 ,
,
则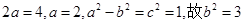 ,
,
∴点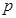 的轨迹方程为
的轨迹方程为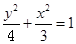 ………………5分
………………5分
曲线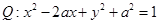 化为
化为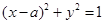 ,
,
则曲线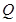 是圆心在
是圆心在 ,半径为1的圆。
,半径为1的圆。
而轨迹E: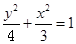 为焦点在y轴上的椭圆短轴上的顶点为
为焦点在y轴上的椭圆短轴上的顶点为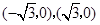 结合它们的图像知:若曲线
结合它们的图像知:若曲线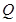 被轨迹E包围着,则
被轨迹E包围着,则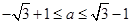 ,
,
∴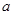 的最小值为
的最小值为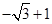 。………………………8分
。………………………8分
(2)设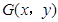 ,由
,由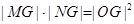 得:
得: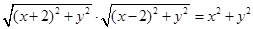 ,
,
化简得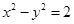 ,即
,即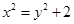 ,
,
而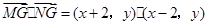
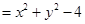
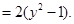 …………10分
…………10分
∵点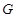 在圆
在圆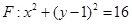 内,∴
内,∴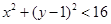
∴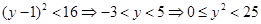 ,
,
∴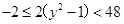 ,
,
∴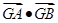 的取值范围为
的取值范围为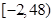 .……………12分
.……………12分
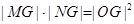 ,得到范围。
,得到范围。(1)由题意得
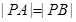 ,∴
,∴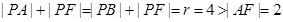
∴P点轨迹是以A、F为焦点的椭圆,进而得到结论。而曲线
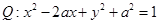 化为
化为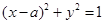 ,
,则曲线
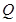 是圆心在
是圆心在 ,半径为1的圆。
,半径为1的圆。,那么利用图像法得到最值。
(2)设
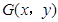 ,由
,由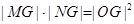 得:
得: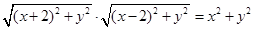 ,
,化简得
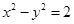 ,即
,即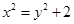 ,
,而
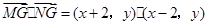
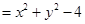
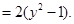
∵点
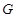 在圆
在圆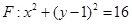 内,∴
内,∴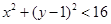 ,得到不等式,然后求解得到。
,得到不等式,然后求解得到。解:(1)由题意得
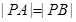 ,∴
,∴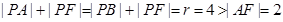
∴P点轨迹是以A、F为焦点的椭圆. ………………………3分
设椭圆方程为
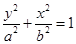
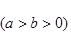 ,
,则
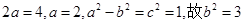 ,
,∴点
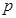 的轨迹方程为
的轨迹方程为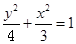 ………………5分
………………5分曲线
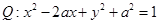 化为
化为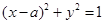 ,
,则曲线
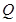 是圆心在
是圆心在 ,半径为1的圆。
,半径为1的圆。而轨迹E:
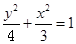 为焦点在y轴上的椭圆短轴上的顶点为
为焦点在y轴上的椭圆短轴上的顶点为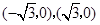 结合它们的图像知:若曲线
结合它们的图像知:若曲线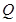 被轨迹E包围着,则
被轨迹E包围着,则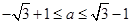 ,
,∴
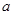 的最小值为
的最小值为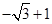 。………………………8分
。………………………8分(2)设
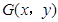 ,由
,由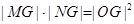 得:
得: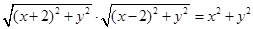 ,
,化简得
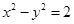 ,即
,即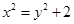 ,
,而
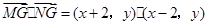
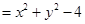
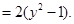 …………10分
…………10分∵点
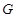 在圆
在圆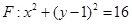 内,∴
内,∴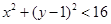
∴
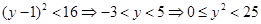 ,
,∴
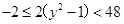 ,
,∴
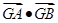 的取值范围为
的取值范围为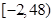 .……………12分
.……………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
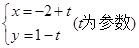 被圆
被圆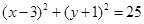 所截得的弦长为( )
所截得的弦长为( ) 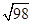
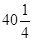
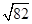
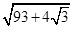
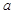 为任意实数时,直线
为任意实数时,直线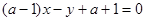 恒过定点
恒过定点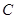 ,则以
,则以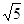 为半径的圆的方程是_____________.
为半径的圆的方程是_____________.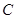 经过
经过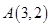 、
、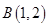 两点,且圆心在直线
两点,且圆心在直线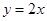 上.
上. 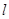 经过点
经过点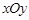 中,圆
中,圆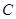 的方程为
的方程为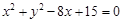 ,若直线
,若直线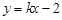 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆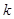 的取值范围是( )
的取值范围是( )
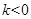 或
或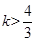
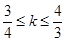
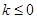 或
或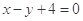 被圆
被圆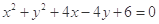 截得的弦长等于( )
截得的弦长等于( )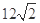
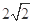
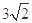
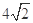
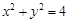 .
.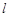 过点P(1,2),且与圆C交于A、B两点,若
过点P(1,2),且与圆C交于A、B两点,若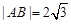 ,求直线
,求直线 ,求动点
,求动点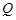 的轨迹方程;
的轨迹方程;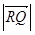 的最小值及相应的
的最小值及相应的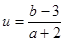 的最大值为__________.
的最大值为__________.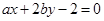
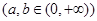 平分圆
平分圆 ,则
,则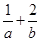 的最小值是
的最小值是