题目内容
若点N(a,b)满足方程关系式a2+b2-4a-14b+45=0,则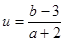 的最大值为__________.
的最大值为__________.
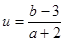 的最大值为__________.
的最大值为__________.
解:方程a2+b2-4a-14b+45=0,即 (a-2)2+(b-7)2=8,表示圆心在(2,7),半径等于2 2 的一个圆.
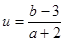 表示圆上的点( a,b)与点(-2,3)连线的斜率.
表示圆上的点( a,b)与点(-2,3)连线的斜率.
设过(-2,3)的圆的切线斜率为 k,则切线方程为 y-3=k(x+2),即 kx-y+2k+3=0,
由圆心到切线的距离等于半径得 |2k-7+2k+3|
 =
= ,解得 k=
,解得 k= ,或 k=
,或 k= ,
,
∴ ≤μ≤
≤μ≤ 故
故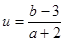 的最大值为
的最大值为 ,
,
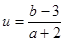 表示圆上的点( a,b)与点(-2,3)连线的斜率.
表示圆上的点( a,b)与点(-2,3)连线的斜率.设过(-2,3)的圆的切线斜率为 k,则切线方程为 y-3=k(x+2),即 kx-y+2k+3=0,
由圆心到切线的距离等于半径得 |2k-7+2k+3|

 =
= ,解得 k=
,解得 k= ,或 k=
,或 k= ,
,∴
 ≤μ≤
≤μ≤ 故
故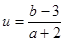 的最大值为
的最大值为 ,
,
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
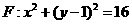 上运动,
上运动,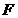 为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹
为圆心,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹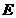 的方程;若曲线
的方程;若曲线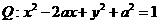 被轨迹
被轨迹 的最小值.(2)已知
的最小值.(2)已知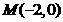 、
、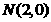 ,动点
,动点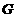 在圆
在圆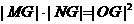 ,求
,求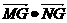 的取值范围.
的取值范围. 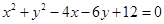 的位置关系是( )
的位置关系是( ) 和圆
和圆 相内切,若
相内切,若 ,且
,且 ,则
,则 的最小值为
的最小值为 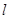 经过点A,且斜率为
经过点A,且斜率为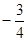 ,
,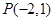 且被圆C:
且被圆C: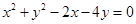 截得弦最长的直线l的方程是( )
截得弦最长的直线l的方程是( ) 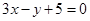
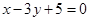
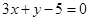
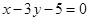
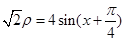 与曲线
与曲线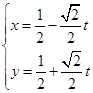 的位置关系是( )。
的位置关系是( )。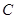 的顶点在坐标原点,准线
的顶点在坐标原点,准线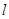 的方程为
的方程为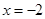 ,点
,点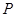 在准线
在准线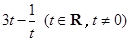 ,点
,点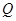 在
在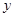 轴上,纵坐标为
轴上,纵坐标为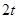 .
.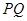 恒与一个圆心在
恒与一个圆心在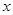 轴上的定圆
轴上的定圆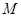 相切,并求出圆
相切,并求出圆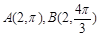 ,C是曲线
,C是曲线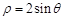 上任意一点,则
上任意一点,则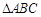 的面积的最小值等于 .
的面积的最小值等于 .