题目内容
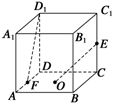
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB, PC的中点 。
(1)求证:EF∥平面PAD;
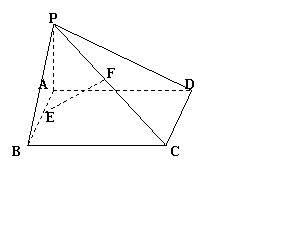
(2)求证:EF⊥CD;
(3)若PA=AD,求二面角P—DC—A的平面角的大小.
证:连AC,设AC中点为O,连OF、OE(1)在△PAC中,∵ F、O分别为PC、AC的中点
∴ FO∥PA …………①在△ABC中,
| |
∵ E、O分别为AB、AC的中点
∴ EO∥BC ,又
 ∵ BC∥AD ∴ EO∥AD …………②
∵ BC∥AD ∴ EO∥AD …………②
综合①、②可知:平面EFO∥平面PAD ∵ EF 平面EFO
∴ EF∥平面PAD.
(2)在矩形ABCD中,∵ EO∥BC,BC⊥CD
∴ EO⊥CD 又 ∵ FO∥PA,PA⊥平面AC ∴ FO⊥平面AC
∴ EO为EF在平面AC内的射影 ∴ CD⊥EF.
(3)PA=AD,则PDA=45,易证所求的二面角为PDA=45。

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 的不等式
的不等式 无解,则实数
无解,则实数 的取值范围是_________
的取值范围是_________ 。
。
 是无理数
是无理数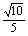 B.
B.  C.
C. 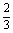 D.
D. 
 上的奇函数
上的奇函数 ,
, ,且对任意不等的正实数
,且对任意不等的正实数 ,
, 都满足
都满足
 ,则不等式
,则不等式 的解集为( ).
的解集为( ).  B.
B.
 D.
D.
 所得的直线方程是( )
所得的直线方程是( )