题目内容
17.若曲线y=$\sqrt{|{{x^2}-9}|}$与直线x+y-m=0有一个交点,则实数m的取值范围是$\left\{{-3}\right\}∪[{0,3})∪({3\sqrt{2},+∞})$.分析 化简曲线y=$\sqrt{|{{x^2}-9}|}$,作出图象,即可得出结论.
解答 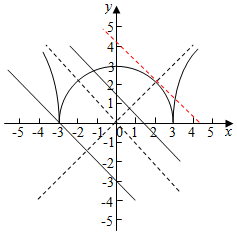 解:x2-9≥0,曲线y=$\sqrt{|{{x^2}-9}|}$,可化为x2-y2=9(y≥0),
解:x2-9≥0,曲线y=$\sqrt{|{{x^2}-9}|}$,可化为x2-y2=9(y≥0),
x2-9<0,曲线y=$\sqrt{|{{x^2}-9}|}$,可化为x2+y2=9(y≥0),
图象如图所示,直线与半圆相切时,m=3$\sqrt{2}$,双曲线的渐近线为y=±x
∴实数m的取值范围是$\left\{{-3}\right\}∪[{0,3})∪({3\sqrt{2},+∞})$.
故答案为:$\left\{{-3}\right\}∪[{0,3})∪({3\sqrt{2},+∞})$.
点评 本题考查曲线与方程,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.函数f(x)=e2+x-2的零点所在的区间是( )
| A. | (-2,-1) | B. | (-1,0) | C. | (1,2) | D. | (0,1) |
9.若{bn}满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x-y≤0}\\{x+y-4≤0}\end{array}\right.$,则z=x+2y的最小值为( )
| A. | 3 | B. | 4 | C. | 7 | D. | 2 |
7.下列向量组中,能作为表示它们所在平面内所有向量的基底的是( )
| A. | $\overrightarrow{a}$=(0,0),$\overrightarrow{b}$=(2,3) | B. | $\overrightarrow{a}$=(1,-3),$\overrightarrow{b}$=(2,-6) | C. | $\overrightarrow{a}$=(4,6),$\overrightarrow{b}$=(6,9) | D. | $\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-4,6) |
 如图所示,AE,DF是圆柱的两条母线,过AD作圆柱的截面交下底面于BC,且AD=BC,圆柱的高为2,底面半径为$\sqrt{3}$
如图所示,AE,DF是圆柱的两条母线,过AD作圆柱的截面交下底面于BC,且AD=BC,圆柱的高为2,底面半径为$\sqrt{3}$