题目内容
若命题“?x∈R,x2+4x+a=0”是真命题,则实数a的取值范围是( )
| A、a≤4 | B、a≥4 |
| C、a<4 | D、a>4 |
考点:特称命题
专题:简易逻辑
分析:根据特称命题的性质,结合一元二次方程的判别式△的关系即可得到结论.
解答:
解:若命题“?x∈R,x2+4x+a=0”是真命题,
则判别式△=16-4a≥0,
解得a≤4,
故选:A.
则判别式△=16-4a≥0,
解得a≤4,
故选:A.
点评:本题主要考查含有量词的命题的应用,结合一元二次方程与判别式之间的关系是解决本题的关键.

练习册系列答案
相关题目
设f(x)=
,则∫
f(x)dx=( )
|
2 0 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知f(x)是R上的奇函数,f(2)=0,xf′(x)-f(x)>0(x>0),则不等式xf(x)>0的解集是( )
| A、(-2,2) |
| B、(-2,0 )∪(0,2) |
| C、(-∞,-2 )∪(2,+∞) |
| D、(-2,0 )∪(2,+∞) |
函数f(x)=x+sinx(x∈R)( )
| A、是偶函数且为减函数 |
| B、是偶函数且为增函数 |
| C、是奇函数且为减函数 |
| D、是奇函数且为增函数 |
已知A={x|-2≤x≤7},B={x|-2≤x≤m+1},且A⊆B,则( )
| A、-2<m≤6 | B、m≥6 |
| C、m=6 | D、m=-3 |
 如图,设正方形ABCD-A1B1C1D1的棱长为1,E,F分别是B1,C1,C1,D1中点,则点A到平面EFDB的距离( )
如图,设正方形ABCD-A1B1C1D1的棱长为1,E,F分别是B1,C1,C1,D1中点,则点A到平面EFDB的距离( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
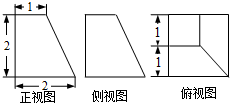 已知台体的体积公式V=
已知台体的体积公式V=