题目内容
 如图,设正方形ABCD-A1B1C1D1的棱长为1,E,F分别是B1,C1,C1,D1中点,则点A到平面EFDB的距离( )
如图,设正方形ABCD-A1B1C1D1的棱长为1,E,F分别是B1,C1,C1,D1中点,则点A到平面EFDB的距离( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:以C为原点,CB、CD、CC1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出点A到平面EFDB的距离.
解答:
解:以C为原点,CB、CD、CC1所在直线分别为x轴,y轴,z轴,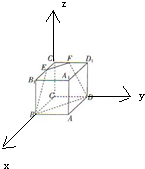
建立空间直角坐标系,
B(1,0,0),E(
,0,1),D(0,1,0),F(0,
,1),A(1,1,0),
∴
=(-
,0,1),
=(0,-
,1),
=(1,0,0),
设平面EFDB的法向量
=(x,y,z),
∴
,
取z=1,则x=y=2,∴
=(2,2,1),
∴点A到平面EFDB的距离:
d=
=
.
故选:B.

建立空间直角坐标系,
B(1,0,0),E(
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BE |
| 1 |
| 2 |
| DF |
| 1 |
| 2 |
| DA |
设平面EFDB的法向量
| n |
∴
|
取z=1,则x=y=2,∴
| n |
∴点A到平面EFDB的距离:
d=
|
| ||||
|
|
| 2 |
| 3 |
故选:B.
点评:本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若命题“?x∈R,x2+4x+a=0”是真命题,则实数a的取值范围是( )
| A、a≤4 | B、a≥4 |
| C、a<4 | D、a>4 |
cos39°cos(-9°)-sin39°sin(-9°)等于( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
在△ABC中,已知|AB|=|BC|=|AC|=2,则向量
与
的数量积
•
=( )
| AB |
| BC |
| AB |
| BC |
A、2
| ||
B、-2
| ||
| C、2 | ||
| D、-2 |
直线l:y=2x-1与圆C:x2+y2=3的位置关系是( )
| A、相离 | B、相切 |
| C、直线过圆C的圆心 | D、相交 |
在下列幂函数中,过点(0,0)和(-1,1),并且是偶函数的是( )
| A、y=-x | ||
| B、y=x-2 | ||
C、y=x
| ||
D、y=x
|
一只昆虫在边长分别为6,8,10的三角形区域内随机爬行,则其到三角形顶点的距离小于2的地方的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设a,b,c均为正数,且(
)a=log2a,(
)b=log
b,2c=log
c,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |