题目内容
6.设函数f(x)=|x-a|+|x-2|.(1)若a=1,解不等式f(x)≤2;
(2)若存在x∈R,使得不等式f(x)≤$\frac{{t}^{2}+4}{t}$对任意t>0恒成立,求实数a的取值范围.
分析 (1)分类讨论,利用绝对值的几何意义得答案;
(Ⅱ)求出f(x)≤$\frac{{t}^{2}+4}{t}$对任意t>0的最小值,f(x)=|x-a|+|x-2|≥|x-a-x+2|=|a-2|,即f(x)的最小值为|a-2|.即可求得实数a的取值范围.
解答 解:(1)当a=1,f(x)=|x-1|+|x-2|.
不等式f(x)>2化为|x-1|+|x-2|≤2.
x<1时,不等式可化为3-2x≤2,∴x≥$\frac{1}{2}$,∴$\frac{1}{2}$≤x<1;
1≤x≤2时,不等式可化为1≤2,成立;
x>2时,不等式可化为2x-3≤2,∴x≤$\frac{5}{2}$,∴2<x≤$\frac{5}{2}$;
综上所述,不等式的解集为[$\frac{1}{2}$,$\frac{5}{2}$];
(2)f(x)=|x-a|+|x-2|≥|x-a-x+2|=|a-2|,即f(x)的最小值为|a-2|.
∵t>0,$\frac{{t}^{2}+4}{t}$=t+$\frac{4}{t}$≥4,当且仅当t=2时,$\frac{{t}^{2}+4}{t}$取得最小值4,
由题意,|a-2|≤4,∴-2≤a≤6.
点评 本题考查函数存在性问题,考查了绝对值不等式的解法,正确理解、运用绝对值的几何意义是解答该题的关键,是中档题.

练习册系列答案
相关题目
16.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的外接球的体积为( )
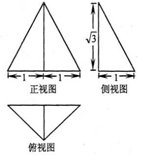

| A. | $\frac{\sqrt{3}}{3}$π | B. | π | C. | $\frac{26}{3}$π | D. | $\frac{32\sqrt{3}}{27}$π |
1.直线2x-y+a=0与3x+y-3=0交于第一象限,当点P(x,y)在不等式组$\left\{\begin{array}{l}{2x-y+a≥0}\\{3x+y-3≤0}\end{array}\right.$表示的区域上运动时,m=4x+3y的最大值为8,此时n=$\frac{y}{x+3}$的最大值是( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |
11.把函数y=sinx(x∈R)的图象上所有点的横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再把所得图象上所有向左平行移动$\frac{π}{3}$个单位长度,得到的图象所表示的函数是( )
| A. | $y=sin(2x-\frac{π}{3}),x∈R$ | B. | $y=sin(\frac{x}{2}+\frac{π}{6}),x∈R$ | C. | $y=sin(2x+\frac{π}{3}),x∈R$ | D. | $y=sin(2x+\frac{2π}{3}),x∈R$ |
16.如图是求样本x1,x2,…,x10平均数$\overline x$的程序框图,图中空白框中应填入的内容为( )
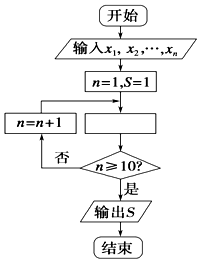

| A. | $S=S+\frac{x_n}{10}$ | B. | $S=S+\frac{x_n}{n}$ | C. | S=S+n | D. | S=S+xn |
 如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,$BD=2\sqrt{3}$,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°.
如图,四边形ABCD中,△BCD为正三角形,AD=AB=2,$BD=2\sqrt{3}$,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°.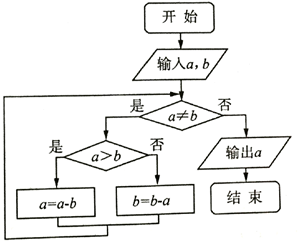 如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a=14,b=21,则输出的a=( )
如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a=14,b=21,则输出的a=( )