题目内容
6.从一副扑克牌(52张)中任抽一张,设A=“抽得老K”,B=“抽得红牌”,C=“抽到J”,判断下列每对事件是否相互独立?是否互斥?是否对立?为什么?(1)A与B;
(2)C与A.
分析 (1)当抽到一当红桃老K和方块老K时,事件A与B能够同时发生,由此能求出结果.
(2)事件C与A不能同时发生,且事件A不发生时,事件C可能发生,也可能不发生,由此能求出结果.
解答 解:(1)∵从一副扑克牌(52张)中任抽一张,
设A=“抽得老K”,B=“抽得红牌”,C=“抽到J”,
∴当抽到一当红桃老K和方块老K时,
事件A与B能够同时发生,且事件A与事件B相互间没有影响,
故事件A与B是相互独立事件,且不是互斥事件,更不是对立事件;
(2)∵A=“抽得老K”,C=“抽到J”,
∴事件C与A不能同时发生,且事件A不发生时,事件C可能发生,也可能不发生,
且A与C相互间没有影响,
∴事件A与C是相互独立事件,且是互斥但不对立事件.
点评 本题考查互斥事件、对立事件的判断,是基础题,解题时要认真审题,注意独立事件、互斥事件、对立事件的定义的合理运用.

练习册系列答案
相关题目
16.下面几种推理过程是演绎推理的是( )
| A. | 某校高三有8个班,1班有51人,2班有53人,由此推断各班人数都超过50人 | |
| B. | 由三角形的性质,推测空间四面体的性质 | |
| C. | 在数列{an}中,a1=1,an+1=$\frac{{a}_{n}}{1+{a}_{n}}$(n=1,2,3),由此归纳出{an}的通项公式 | |
| D. | 三角函数都是周期函数,tanα是三角函数,因此tanα是周期函数 |
17.若等比数列{an}的各项均为正数,a4a17+a9a12=64,则log2a1+log2a2+…+log2a20=( )
| A. | 50 | B. | 60 | C. | 100 | D. | 120 |
11.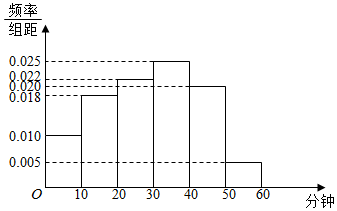 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(2)现从课外体育达标学生中按分层抽样抽取5人,再从这5名学生中随机抽取2人参加体育知识问卷调查,求抽取的这2人课外锻炼时间都在[40,50)内的概率.
附参考公式与数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 60 | 30 | 90 |
| 女 | 90 | 20 | 110 |
| 合计 | 150 | 50 | 200 |
附参考公式与数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
18.已知集合A={x∈R|0<log2x<1},B={y∈R|y=2-x2},则A∩B=( )
| A. | ∅ | B. | (0,2] | C. | (1,2) | D. | (1,2] |