题目内容
设A是整数集的一个非空子集，若集合A满足：①?k∈A，k+1∈A；②对于?k∈A，都有k-2∉A，此时就称集合A具备M性质．给定S={1，2，3，4，5，6}，由S的3个元素构成的所有集合中，具备M性质的集合共有 个．
考点：子集与真子集
专题：集合
分析：由题意直接写出满足题意的集合即可．
解答：
解：S={1，2，3，4，5，6}，由S的3个元素构成的所有集合中，满足：①?k∈A，k+1∈A；②对于?k∈A，都有k-2∉A，
符合题意的集合是：{1，2，5}，{1，2，6}，{2，3，6}，{1，4，5}，{1，5，6}，{2，5，6}，共6个．
故答案为：6．
符合题意的集合是：{1，2，5}，{1，2，6}，{2，3，6}，{1，4，5}，{1，5，6}，{2，5，6}，共6个．
故答案为：6．
点评：本题考查集合的基本性质的应用，基本知识的考查．
练习册系列答案
相关题目
已知双曲线
-
=1的右焦点为（3，0），则a的值等于（ ）
| x2 |
| a2 |
| y2 |
| 5 |
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、
|
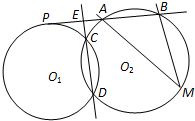已知⊙O1和⊙O2交于点C和D，⊙O1上的点P处的切线交⊙O2于A、B点，交直线CD于点E，M是⊙O2上的一点，若PE=2，EA=1，∠AMB=45°，那么⊙O2的半径为若A={（2，-2），（2，2）}，则集合A中元素的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |