题目内容
已知Sn是等比数列{an}的前n项和,S3+2,S9+2,S6+2成等差数列,且a2+a5=4.
(Ⅰ)求数列{an}的公比q;
(Ⅱ)设bn=log2|an|,求数列{bn}的前n项和Tn.
(Ⅰ)求数列{an}的公比q;
(Ⅱ)设bn=log2|an|,求数列{bn}的前n项和Tn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(I)设等比数列{an}的公比为q,当q≠1时,由S3+2,S9+2,S6+2成等差数列,且a2+a5=4.可得2(S9+2)=S6+2+S3+2,a1(q+q4)=4.利用等比数列的前n项和公式化简解出即可.当q=1时,不满足条件,舍去.
(II)(II)由(I)可得an=a2qn-2=(-1)n-2•2
.可得bn=log2|an|=
.,对n分类讨论;当n≤11时,当n≥12时,利用等差数列的前n项和公式即可得出,
(II)(II)由(I)可得an=a2qn-2=(-1)n-2•2
| 11-n |
| 3 |
|
解答:
解:(I)设等比数列{an}的公比为q,
当q≠1时,∵S3+2,S9+2,S6+2成等差数列,且a2+a5=4.
∴2(S9+2)=S6+2+S3+2,a1(q+q4)=4.
∴2×
=
+
,
化为(2q3+1)(q3-1)=0.
解得q3=-
.a2=8.
当q=1时,不满足条件,舍去.
∴q=-
.
(II)由(I)可得an=a2qn-2=(-1)n-2•2
.
bn=log2|an|=
.,
当n≤11时,数列{bn}的前n项和Tn=
=
.
当n≥12时,数列{bn}的前n项和Tn=T11+
+
+…+
.
=
+
×[
-11×(n-11)]
=
.
当q≠1时,∵S3+2,S9+2,S6+2成等差数列,且a2+a5=4.
∴2(S9+2)=S6+2+S3+2,a1(q+q4)=4.
∴2×
| a1(q9-1) |
| q-1 |
| a1(q6-1) |
| q-1 |
| a1(q3-1) |
| q-1 |
化为(2q3+1)(q3-1)=0.
解得q3=-
| 1 |
| 2 |
当q=1时,不满足条件,舍去.
∴q=-
| 3 |
| ||
(II)由(I)可得an=a2qn-2=(-1)n-2•2
| 11-n |
| 3 |
bn=log2|an|=
|
当n≤11时,数列{bn}的前n项和Tn=
11(
| ||||
| 2 |
| -n2+21n |
| 6 |
当n≥12时,数列{bn}的前n项和Tn=T11+
| 12-11 |
| 3 |
| 13-11 |
| 3 |
| n-11 |
| 3 |
=
| 21×11-112 |
| 6 |
| 1 |
| 3 |
| (n-11)(12+n) |
| 2 |
=
| n2-21n+220 |
| 6 |
点评:本题考查了等差数列与等比数列的通项公式及其前n项和公式、对数的运算性质,考查了分类讨论思想方法,考查了分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
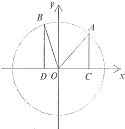 如图,在平面直角坐标系xOY中,点A(x1,y1)在单位圆O上.∠xOA=α且α∈(
如图,在平面直角坐标系xOY中,点A(x1,y1)在单位圆O上.∠xOA=α且α∈( 已知函数f(x)=
已知函数f(x)=
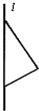
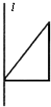
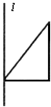
 要得到如图所示的几何体,只需将图所示的三角形绕直线l旋转一周,则可以是( )
要得到如图所示的几何体,只需将图所示的三角形绕直线l旋转一周,则可以是( )