题目内容
(本小题满分16分)已知椭圆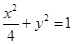 中心为
中心为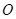 ,右顶点为
,右顶点为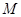 ,过定点
,过定点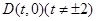 作
作 直线
直线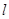 交椭圆于
交椭圆于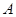 、
、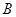 两点.
两点.
(1)若直线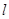 与
与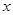 轴垂直,求三角形
轴垂直,求三角形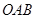 面积的最大值;
面积的最大值;
(2)若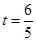 ,直线
,直线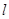 的斜率为
的斜率为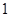 ,求证:
,求证: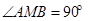 ;
;
(3)在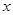 轴上,是否存在一点
轴上,是否存在一点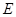 ,使直线
,使直线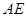 和
和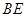 的斜率的乘积为非零常数?若存在,求出点
的斜率的乘积为非零常数?若存在,求出点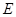 的坐标和这个常数;若不存在,说明理由.
的坐标和这个常数;若不存在,说明理由.
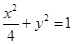 中心为
中心为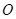 ,右顶点为
,右顶点为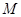 ,过定点
,过定点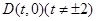 作
作 直线
直线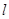 交椭圆于
交椭圆于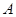 、
、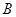 两点.
两点.(1)若直线
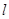 与
与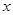 轴垂直,求三角形
轴垂直,求三角形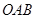 面积的最大值;
面积的最大值;(2)若
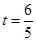 ,直线
,直线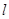 的斜率为
的斜率为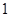 ,求证:
,求证: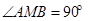 ;
;(3)在
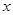 轴上,是否存在一点
轴上,是否存在一点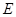 ,使直线
,使直线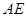 和
和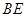 的斜率的乘积为非零常数?若存在,求出点
的斜率的乘积为非零常数?若存在,求出点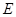 的坐标和这个常数;若不存在,说明理由.
的坐标和这个常数;若不存在,说明理由.解:设直线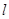 与椭圆的交点坐标为
与椭圆的交点坐标为 .
.
(1)把 代入
代入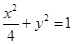 可得:
可得: , (2分)
, (2分)
则 ,当且仅当
,当且仅当 时取等号 (4分)
时取等号 (4分)
(2)由 得
得 ,
, ,
, (6分)
(6分)
所以



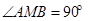 (9分)
(9分)
(3)(理)当直线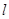 与
与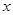 轴不垂直时,可设直线方程为:
轴不垂直时,可设直线方程为: ,
,
由 消去
消去 整理得
整理得
则 ① 又
① 又  ②
②
若存在定点 符合题意,且
符合题意,且
 (11分)
(11分)
把①、②式代入上式整理得
 (其中
(其中 都是常数)
都是常数)
要使得上式对变量 恒成立,当且仅当
恒成立,当且仅当
 ,解得
,解得 (13分)
(13分)
当 时,定点
时,定点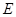 就是椭圆的右顶点
就是椭圆的右顶点 ,此时,
,此时, ;
;
当 时,定点
时,定点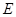 就是椭圆的左顶点
就是椭圆的左顶点 ,此时,
,此时, ; (15分)
; (15分)
当直线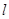 与
与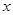 轴垂直时,由
轴垂直时,由 ,解得两交点坐标为
,解得两交点坐标为
 ,可验证:
,可验证: 或
或
所以,存在一点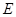
 (或
(或 ),使直线
),使直线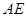 和
和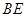 的斜率的乘积为
的斜率的乘积为
非零常数 (或
(或 ). (16分)
). (16分)
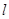 与椭圆的交点坐标为
与椭圆的交点坐标为 .
.(1)把
 代入
代入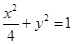 可得:
可得: , (2分)
, (2分)则
 ,当且仅当
,当且仅当 时取等号 (4分)
时取等号 (4分)(2)由
 得
得 ,
, ,
, (6分)
(6分)所以




 (9分)
(9分)(3)(理)当直线
 与
与 轴不垂直时,可设直线方程为:
轴不垂直时,可设直线方程为: ,
,由
 消去
消去 整理得
整理得
则
 ① 又
① 又  ②
② 若存在定点
 符合题意,且
符合题意,且
 (11分)
(11分)把①、②式代入上式整理得
 (其中
(其中 都是常数)
都是常数)要使得上式对变量
 恒成立,当且仅当
恒成立,当且仅当 ,解得
,解得 (13分)
(13分)当
 时,定点
时,定点 就是椭圆的右顶点
就是椭圆的右顶点 ,此时,
,此时, ;
; 当
 时,定点
时,定点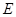 就是椭圆的左顶点
就是椭圆的左顶点 ,此时,
,此时, ; (15分)
; (15分)当直线
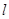 与
与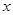 轴垂直时,由
轴垂直时,由 ,解得两交点坐标为
,解得两交点坐标为 ,可验证:
,可验证: 或
或
所以,存在一点
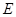
 (或
(或 ),使直线
),使直线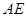 和
和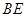 的斜率的乘积为
的斜率的乘积为非零常数
 (或
(或 ). (16分)
). (16分)略

练习册系列答案
相关题目
 是椭圆
是椭圆 的左、右焦点,点
的左、右焦点,点 在椭圆上运动,则
在椭圆上运动,则 的最大值是_____
的最大值是_____ )的距离比它到X轴的距离多
)的距离比它到X轴的距离多 与曲线C交于A、B两点,若
与曲线C交于A、B两点,若  为正三角形,求M点的坐标与直线
为正三角形,求M点的坐标与直线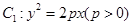 的焦点
的焦点 以及椭圆
以及椭圆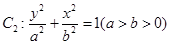 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆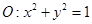 上.
上. 和椭圆
和椭圆 的标准方程;
的标准方程;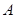 、
、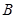 两不同点,交
两不同点,交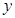 轴于点
轴于点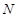 ,已知
,已知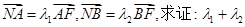 为定值.
为定值.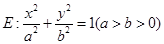 的左右焦点为
的左右焦点为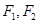 ,过点
,过点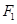 且斜率为正数的直线
且斜率为正数的直线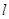 交椭圆
交椭圆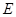 于
于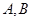 两点,且
两点,且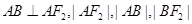 成等差数列。
成等差数列。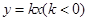 与椭圆
与椭圆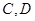 两点,求使四边形
两点,求使四边形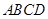 的面积最大时的
的面积最大时的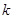 值。
值。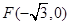 ,右顶点为
,右顶点为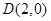 ,设点
,设点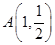 .(1)求该椭圆的标准方程;
.(1)求该椭圆的标准方程; 是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点
是椭圆上的动点,过P点向椭圆的长轴做垂线,垂足为Q求线段PQ的中点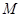 的轨迹方程;
的轨迹方程;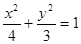 的焦距等于
的焦距等于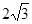
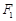 、
、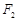 是椭圆C:
是椭圆C: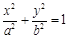 (
(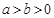 )的两个焦点,P为椭圆C上的一点,且
)的两个焦点,P为椭圆C上的一点,且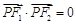 。若
。若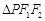 的面积为9,则
的面积为9,则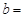 _________。
_________。