题目内容
. (本小题满分12分)已知抛物线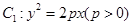 的焦点
的焦点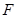 以及椭圆
以及椭圆
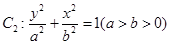 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆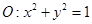 上.
上.
(1)求抛物线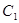 和椭圆
和椭圆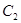 的标准方程;
的标准方程;
(2)过点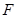 的直线交抛物线
的直线交抛物线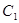 于
于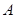 、
、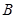 两不同点,交
两不同点,交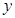 轴于点
轴于点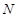 ,已知
,已知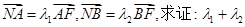 为定值.
为定值.
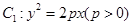 的焦点
的焦点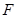 以及椭圆
以及椭圆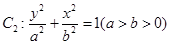 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆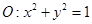 上.
上.(1)求抛物线
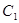 和椭圆
和椭圆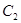 的标准方程;
的标准方程;(2)过点
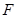 的直线交抛物线
的直线交抛物线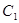 于
于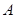 、
、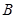 两不同点,交
两不同点,交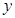 轴于点
轴于点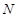 ,已知
,已知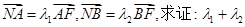 为定值.
为定值.解:(Ⅰ)由
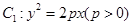 焦点
焦点 在圆
在圆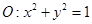 上得:
上得: \
\所以抛物线
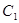 :
:
同理由椭圆
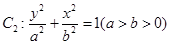 的上、下焦点
的上、下焦点 及左、右顶点
及左、右顶点 均在圆
均在圆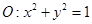 上可解得:
上可解得:
得椭圆
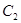 :
:
总之,抛物线
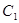 :
: 、椭圆
、椭圆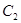 :
:
(Ⅱ)设直线
 的方程为
的方程为 ,
, ,则
,则 .
. 联立方程组
 消去
消去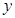
得:
 ,
, , 故
, 故
由
 ,
, 得,
得,
整理得,
 ,
,
略

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
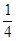 .
.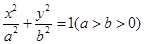 的左顶点为
的左顶点为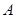 ,左焦点为
,左焦点为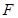 ,上顶点为
,上顶点为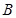 ,若
,若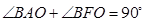 ,则该椭圆的离心率是 .
,则该椭圆的离心率是 .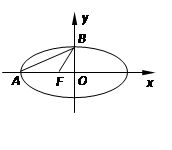
 轴上,短轴长为4,离心率为
轴上,短轴长为4,离心率为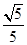 .
.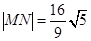 ,求直线l的方程.
,求直线l的方程.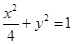 中心为
中心为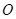 ,右顶点为
,右顶点为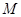 ,过定点
,过定点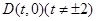 作
作 直线
直线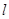 交椭圆于
交椭圆于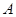 、
、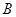 两点.
两点.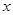 轴垂直,求三角形
轴垂直,求三角形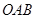 面积的最大值;
面积的最大值;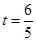 ,直线
,直线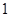 ,求证:
,求证: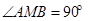 ;
;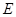 ,使直线
,使直线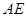 和
和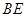 的斜率的乘积为非零常数?若存在,求出点
的斜率的乘积为非零常数?若存在,求出点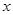 轴上的椭圆,离心率
轴上的椭圆,离心率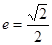 ,且经过抛物线
,且经过抛物线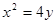 的焦点.
的焦点.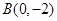 的直线
的直线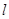 (斜率不等于零)与椭圆交于不同的两点
(斜率不等于零)与椭圆交于不同的两点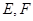 (
(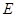 在
在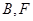
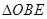 与
与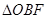 面积之比为
面积之比为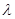 ,求
,求 是椭圆的两焦点,
是椭圆的两焦点, 为椭圆上一点,若
为椭圆上一点,若 ,则离心率
,则离心率 的最小值是_______
的最小值是_______ 的焦点坐标是( )
的焦点坐标是( )



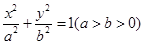 与
与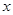 轴交于
轴交于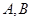 两点,两焦点将线段
两点,两焦点将线段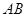 三等分,焦距为
三等分,焦距为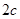 ,椭圆上一点
,椭圆上一点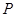 到左焦点的距离为
到左焦点的距离为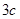 ,则
,则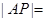 ___________.
___________.