题目内容
函数y=
的单调递增区间是（ ）
| lnx |
| x |
| A、（e，+∞） |
| B、（-∞，e） |
| C、（e-1，+∞） |
| D、（0，e） |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：求出函数函数f（x）的导数，令f′（x）＞0 求得x的范围，即可得到函数f（x）的单调递增区间．
解答：
解：∵y=
，x＞0，
∴y′=
，
令y′＞0 可得 lnx＜1，解得0＜x＜e，
故函数y=
的单调递增区间是（0，e）．
故选：D．
| lnx |
| x |
∴y′=
| 1-lnx |
| x2 |
令y′＞0 可得 lnx＜1，解得0＜x＜e，
故函数y=
| lnx |
| x |
故选：D．
点评：本题主要考查利用导数研究函数的单调性，属于基础题．
练习册系列答案
相关题目
已知集合M={x|x＞1}，N={x|x2≤4}，则M∩N=（ ）
| A、（1，2） |
| B、[1，2] |
| C、（1，2] |
| D、[-2，+∞） |
设m，n是两条不同的直线，α，β，γ是三个不同的平面．有下列四个命题：
①若m?β，α⊥β，则m⊥α
②若α∥β，m?α，则m∥β
③若n⊥α，n⊥β，m⊥α则m⊥β
④若α⊥γ，β⊥γ，则α⊥β
其中正确命题的序号是（ ）
①若m?β，α⊥β，则m⊥α
②若α∥β，m?α，则m∥β
③若n⊥α，n⊥β，m⊥α则m⊥β
④若α⊥γ，β⊥γ，则α⊥β
其中正确命题的序号是（ ）
| A、①③ | B、①② | C、③④ | D、②③ |
在（1-x）20的展开式中，如果第4r项和第r+2项的二项式系数相等，则r的值为（ ）
| A、4 | B、5 | C、6 | D、7 |
函数y=sin2x的一个单调递增区间可以是（ ）
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
| D、[0，π] |
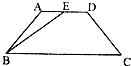如图，在等腰梯形ABCD中，下底BC长为3，底角C为45°，高为a，E为上底AD的中点，F为折线段C-D-A上的动点，设| BE |
| BF |
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
已知直线a与直线b是异面直线，过空间一定点P（点P不在直线a与直线b上）作与直线a、直线b都平行的平面有（ ）
| A、有且只有一个 |
| B、不存在或者有一个 |
| C、有无数个 |
| D、恰有两个 |