题目内容

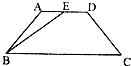如图，在等腰梯形ABCD中，下底BC长为3，底角C为45°，高为a，E为上底AD的中点，F为折线段C-D-A上的动点，设
BE
•
BF
的最小值为g（a），若关于a的方程g（a）=ka-1有两个不相等的实根，则实数k的取值范围为（　　）
A、（
7
2
，
11
3
）
B、（
7
2
，+∞）
C、（
11
3
，+∞）
D、（
13
，+∞）
考点：平面向量的综合题,平面向量数量积的运算
专题：平面向量及应用
分析：以A为坐标原点，以BC方向为x轴正方向建立空间坐标系，结合F为折线段C-D-A上的动点，可得当F落在A点时，
BE
•
BF
取最小值g（a）=a2+
3
2
a，（0＜a＜
3
2
），若关于a的方程g（a）=ka-1有两个不相等的实根，则
△=(
3
2
-k)2-4＞0
0＜
k-
3
2
2
＜
3
2
(
3
2
)2+
3
2
(
3
2
-k)+1＞0
，解不等式组，可得实数k的取值范围．
解答： 解：以B为坐标原点，以BC方向为x轴正方向建立空间坐标系，
由已知可得：A（a，a），C（3，0），E（
3
2
，a），
由F为折线段C-D-A上的动点，
故当F落在A点时，
BE
•
BF
取最小值g（a），
即g（a）=（
3
2
，a）•（a，a）=a2+
3
2
a，（0＜a＜
3
2
）
若关于a的方程g（a）=ka-1有两个不相等的实根，
即a2+（
3
2
-k）a+1=0在（0，
3
2
）上有两个不等式相等的实根，
故
△=(
3
2
-k)2-4＞0
0＜
k-
3
2
2
＜
3
2
(
3
2
)2+
3
2
(
3
2
-k)+1＞0

解得：k∈（
7
2
，
11
3
），
故选：A
点评：本题考查的知识点是平面向量及应用，方程根的存在性及个数判断，是方程，向量，不等式的综合应用，难度较大．
练习册系列答案
相关题目
若二项式（ax-
1
x
）6的展开式中的常数项为-160，则
∫
a
0
（3x2-1）dx=
 
．
函数y=
lnx
x
的单调递增区间是（　　）
A、（e，+∞）
B、（-∞，e）
C、（e-1，+∞）
D、（0，e）
若集合A={x||x-2|≤3，x∈R}，B={y|y=lg（x-1）}，则A∩B=（　　）
A、[-1，1）
B、（-∞，1）
C、[-1，5]
D、（1，5]
已知函数f（x）=
2x-2，x≤1
2+log2x，x＞1
，则函数f（x）的零点为（　　）
A、
1
4
和1
B、-4和0
C、
1
4
D、1
在一次智力竞赛中，每位参赛者要从5道题中不放回地依次抽取2道题作答，已知5道题中包含自然科学题3道，人文科学题2道．则参赛者甲在第一次抽到自然科学题的条件下，第二次还抽到自然科学题的概率是（　　）
A、
3
10
B、
1
2
C、
3
5
D、
2
5
已知圆O的方程为x2+y2=4，向量
OA
=（1，0），
OB
=（3，0），点P是圆O上任意一点，那么
PA
•
PB
的取值范围是（　　）
A、（-1，11）
B、（-1，15）
C、[-5，11]
D、[-1，15]
已知直线l：x-y+4=0与圆C：（x-1）2+（y-1）2=2，则圆C上各点到l的距离的最小值为（　　）
A、
2
B、
3
C、1
D、3
如图，在复平面内，复数z1和z2对应的点分别是A和B，则
z1
z2
=（　　）
A、
1
3
-
2
3
i
B、-
1
3
+
2
3
i
C、
1
5
-
2
5
i
D、-
1
5
+
2
5
i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网