题目内容
6.下列各组空间向量相互垂直的是( )| A. | $\overrightarrow{a}$=(0,1,-2),$\overrightarrow{b}$=(2,0,-1) | B. | $\overrightarrow{a}$=(3,-1,1),$\overrightarrow{b}$=(-1,0,3) | ||
| C. | $\overrightarrow{a}$=(0,-1,-2),$\overrightarrow{b}$=(0,-2,4) | D. | $\overrightarrow{a}$=(3,-1,1),$\overrightarrow{b}$=(-3,1,-1) |
分析 根据$\overrightarrow{a}$•$\overrightarrow{b}$=0,即可判断$\overrightarrow{a}$⊥$\overrightarrow{b}$成立.
解答 解:对于A,$\overrightarrow{a}$•$\overrightarrow{b}$=0+0+2=2≠0,∴$\overrightarrow{a}$⊥$\overrightarrow{b}$不成立;
对于B,$\overrightarrow{a}$•$\overrightarrow{b}$=-3+0+3=0,∴$\overrightarrow{a}$⊥$\overrightarrow{b}$成立;
对于C,$\overrightarrow{a}$•$\overrightarrow{b}$=0+2-8=-6≠0,∴$\overrightarrow{a}$⊥$\overrightarrow{b}$不成立;
对于D,$\overrightarrow{a}$•$\overrightarrow{b}$=-9-1-1=-11≠0,∴$\overrightarrow{a}$⊥$\overrightarrow{b}$不成立.
故选:B.
点评 本题考查了利用向量的数量积判断两向量是否垂直的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若$sinA=\frac{{2\sqrt{2}}}{3}$,a=2,ccosB+bcosC=2acosB,则b的值为( )
| A. | $2\sqrt{6}$ | B. | $\frac{{3\sqrt{2}}}{4}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $\frac{{3\sqrt{6}}}{4}$ |
17.某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
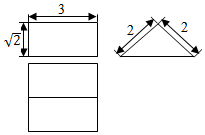

| A. | $\frac{17\sqrt{17}}{6}$π | B. | 34π | C. | 17π | D. | $\frac{17}{4}$π |
1.下列命题为真命题的是( )
| A. | 已知x,y∈R,则$\left\{\begin{array}{l}{x>1}\\{y>2}\end{array}\right.$是$\left\{\begin{array}{l}{x+y>3}\\{xy>2}\end{array}\right.$的充要条件 | |
| B. | 对空间任意一点O与不共线的三点A,B,C,若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{Ob}+z\overrightarrow{OC}$(其中x,y,z∈R),则P,A,B,C四点共面 | |
| C. | ?a,b∈R,$\frac{a+b}{2}≥\sqrt{ab}$ | |
| D. | ?x∈R,sinx+cosx=$\frac{7}{5}$ |
11.直线3x+4y+2m=0与圆x2+(y-$\frac{1}{2}$)2=1相切,且实数m的值为( )
| A. | log23 | B. | 2 | C. | log25 | D. | 3 |
15.已知数列{an}是递增的等比数列,a1+a5=17,a2a4=16,则公比q=( )
| A. | -4 | B. | 4 | C. | -2 | D. | 2 |
