题目内容

15．已知数列{an}是递增的等比数列，a1+a5=17，a2a4=16，则公比q=（　　）
A．-4B．4C．-2D．2

分析 设等比数列{an}是公比为q的递增的等比数列，运用等比数列的性质，求得a1=1，a5=16，再由等比数列的通项公式求得公比即可．

解答 解：设等比数列{an}是公比为q的递增的等比数列，
由a2a4=16，可得a1a5=16，
又a1+a5=17，解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{{a}_{5}=16}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=16}\\{{a}_{5}=1}\end{array}\right.$（不合题意，舍去），
即有q4=16，解得q=2（负的舍去）．
故选：D．

点评 本题考查等比数列的通项公式的运用，是基础题．

练习册系列答案
相关题目
5．已知圆C：x2+y2-6x-8y-5t=0，直线l：x+3y+15=0．
（1）若直线l被圆C截得的弦长为$2\sqrt{10}$，求实数t的值；
（2）当t=1时，由直线l上的动点P引圆C的两条切线，若切点分别为A，B，则在直线AB上是否存在一个定点？若存在，求出该定点的坐标；若不存在，请说明理由．
6．下列各组空间向量相互垂直的是（　　）
A．$\overrightarrow{a}$=（0，1，-2），$\overrightarrow{b}$=（2，0，-1）B．$\overrightarrow{a}$=（3，-1，1），$\overrightarrow{b}$=（-1，0，3）
C．$\overrightarrow{a}$=（0，-1，-2），$\overrightarrow{b}$=（0，-2，4）D．$\overrightarrow{a}$=（3，-1，1），$\overrightarrow{b}$=（-3，1，-1）
3．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（0，1），离心率为$\frac{\sqrt{6}}{3}$，长轴的端点为A1，A2，动直线l：y=kx+m（k≠0）与椭圆相切于点P，直线PA1，PA2的斜率分别为k1，k2．
（1）求椭圆的方程；
（2）求证：$\frac{{k}_{1}+{k}_{2}}{k}$为定值．
10．已知数列{an}的通项公式为an=$\frac{n}{n+1}$，则数列{an}是（　　）
A．递减数列B．递增数列C．常数列D．摆动数列
20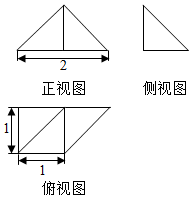．如图是一个几何体的三视图，正视图是一个等腰直角三角形，侧视图为一个直角三角形，俯视图是一个直角梯形，则此几何体的表面积是（　　）
A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．$\frac{5+\sqrt{3}}{2}$D．$\frac{5+\sqrt{3}}{2}$+$\sqrt{2}$
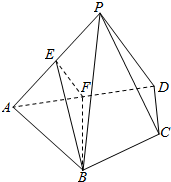7．如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB=AD=4AP，∠BAD=∠PAD=60°，E，F分别是AP，AD的中点．
（1）求证：平面BEF⊥平面PAD；
（2）求二面角P-BE-F的正切值．
4．若向量$\overrightarrow{a}$=（1，1），$\overrightarrow{b}$=（2，5），$\overrightarrow{c}$=（3，x）．
（1）若$\overrightarrow{b}$∥$\overrightarrow{c}$，求x的值；
（2）若（8$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{c}$=30，求x的值．
5．已知某几何体的三视图如图所示，则该几何体的体积为（　　）
A．48B．4C．12D．16

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网