题目内容
16.如图,曲线y=f(x)在点P处的切线方程是y=-x+10,则f(7)+f′(7)=2.
分析 根据导数的几何意义进行求解判断即可.
解答 解:∵曲线y=f(x)在点P处的切线方程是y=-x+10,
∴当x=7时,y=-7+10=3,即f(7)=3,
同时切线的斜率k=f′(7)=-1,
则f(7)+f′(7)=3-1=2,
故答案为:2.
点评 本题主要考查导数的几何意义,根据切点,切线斜率与导数的关系是解决本题的关键.比较基础.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
6.下列各组空间向量相互垂直的是( )
| A. | $\overrightarrow{a}$=(0,1,-2),$\overrightarrow{b}$=(2,0,-1) | B. | $\overrightarrow{a}$=(3,-1,1),$\overrightarrow{b}$=(-1,0,3) | ||
| C. | $\overrightarrow{a}$=(0,-1,-2),$\overrightarrow{b}$=(0,-2,4) | D. | $\overrightarrow{a}$=(3,-1,1),$\overrightarrow{b}$=(-3,1,-1) |
11.对于数25,规定第1次操作为23+53=133,第2次操作为13+33+33=55,如此反复操作,则第2016次操作后得到的数是( )
| A. | 25 | B. | 250 | C. | 55 | D. | 133 |
5.已知某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 48 | B. | 4 | C. | 12 | D. | 16 |
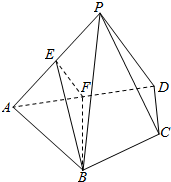 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD=4AP,∠BAD=∠PAD=60°,E,F分别是AP,AD的中点.