题目内容
12.已知函数f(x)=$\frac{a(x-1)}{{x}^{2}}$,其中a>0.(1)求函数f(x)的单调区间;
(2)设g(x)=xlnx-x2f(x),求g(x)在区间[1,e]上的最小值(其中e为自然对数的底数)
分析 (1)求导数,利用导数求函数的单调性区间;
(2)利用导数求函数g(x)在闭区间上的最小值.
解答 解:(1)f′(x)=$\frac{a({-x}^{2}+2x)}{{x}^{4}}$,(x≠0),
因为a>0,所以由f′(x)>0,-x2+2x>0得0<x<2,此时函数单调递增.
由f′(x)<0,得-x2+2x<0,即x>2或x<0,此时函数单调递减.
所以函数f(x)的单调递减区间为(-∞,0)和(2,+∞),单调递增区间为(0,2).
(2)g(x)=xlnx-x2f(x)=xlnx-a(x-1),
则g'(x)=lnx+1-a,由g'(x)=lnx+1-a=0,解得x=ea-1.
所以在区间(0,ea-1)上,函数单调递减,在(ea-1.,+∞)上,函数单调递增.
①当ea-1.≤1,即0<a≤1时,在区间[l,e]上g(x)单调递增,所以g(x)的最小值为g(1)=0.
②当ea-1.≥e,即a≥2时,在区间[l,e]上g(x)单调递减,所以g(x)的最小值为g(e)=e+a-ae.
③当1<ea-1.<e,即1<a<2时,g(x)的最小值为g(ea-1)=(a-1)ea-1-a(ea-1-1)=a-ea-1.
综上当0<a≤1时,g(x)的最小值为g(1)=0.
当1<a<2时,g(x)的最小值为g(ea-1),
当≥2时,g(x)的最小值为g(e)=e+a-ae.
点评 本题主要考查利用导数研究函数的最值和函数的单调区间,比较综合.

练习册系列答案
相关题目
5.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有垣厚五尺,两鼠对穿.大鼠日一尺,小鼠亦日一尺.大鼠日自倍,小鼠日自半.问几何日相逢?各穿几何?”,翻译成今天的话是:一只大鼠和一只小鼠分别从的墙两侧面对面打洞,已知第一天两鼠都打了一尺长的洞,以后大鼠每天打的洞长是前一天的2倍,小鼠每天打的洞长是前一天的一半,已知墙厚五尺,问两鼠几天后相见?相见时各打了几尺长的洞?设两鼠x 天后相遇(假设两鼠每天的速度是匀速的),则x=( )
| A. | $2\frac{1}{18}$ | B. | $2\frac{1}{17}$ | C. | $2\frac{2}{17}$ | D. | $2\frac{1}{9}$ |
6.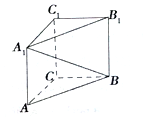 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=AC=BC=1,则异面直线A1B与AC所成角的余弦值是( )| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
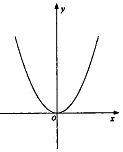 已知点$A({2\sqrt{2},2})$在抛物线C:x2=2py(p>0)上.
已知点$A({2\sqrt{2},2})$在抛物线C:x2=2py(p>0)上.