题目内容
5.所sinα=-$\frac{4}{5}$,且α是第三象限角,求:(1)sin($\frac{π}{4}$+α);
(2)cos($\frac{π}{4}$+α);
(3)tan($\frac{π}{4}$+α).
分析 由已知求出cosα,tanα.
(1)展开两角和的正弦得答案;
(2)展开两角和的余弦得答案;
(3)展开两角和的正切得答案.
解答 解:∵sinα=-$\frac{4}{5}$,且α是第三象限角,
∴cos$α=-\frac{3}{5}$,tanα=$\frac{4}{3}$.
(1)sin($\frac{π}{4}$+α)=sin$\frac{π}{4}$cosα+cos$\frac{π}{4}$sinα=$\frac{\sqrt{2}}{2}×(-\frac{3}{5})+\frac{\sqrt{2}}{2}×(-\frac{4}{5})=-\frac{7\sqrt{2}}{10}$;
(2)cos($\frac{π}{4}$+α)=cos$\frac{π}{4}$cosα-sin$\frac{π}{4}$sinα=$\frac{\sqrt{2}}{2}×(-\frac{3}{5})-\frac{\sqrt{2}}{2}×(-\frac{4}{5})=\frac{\sqrt{2}}{10}$;
(3)tan($\frac{π}{4}$+α)=$\frac{tan\frac{π}{4}+tanα}{1-tan\frac{π}{4}tanα}$=$\frac{1+\frac{4}{3}}{1-1×\frac{4}{3}}$=-7.
点评 本题考查三角函数的化简求值,考查两角和与差的三角函数,是基础的计算题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
19.在△ABC中,D为BC上的点,AD平分∠BAC,且△ABD的面积是△ACD的面积的一半.
(Ⅰ)求$\frac{sin∠B}{sin∠C}$的值;
(Ⅱ)若∠BAC=120°,AD=1,求AC的长.
(Ⅰ)求$\frac{sin∠B}{sin∠C}$的值;
(Ⅱ)若∠BAC=120°,AD=1,求AC的长.
16.设首项为1,公比为$\frac{1}{3}$的等比数列{an}的前n项和Sn,则Sn=( )
| A. | $\frac{3-2{a}_{n}}{2}$ | B. | $\frac{2{a}_{n}-3}{2}$ | C. | $\frac{3-{a}_{n}}{2}$ | D. | $\frac{{a}_{n}-3}{2}$ |
14.若函数f(x)=sin2x+4cosx+ax在R上单调递减,则实数a的取值范围是( )
| A. | (-∞,-3] | B. | (-∞,-3) | C. | (-∞,6] | D. | (-∞,6) |
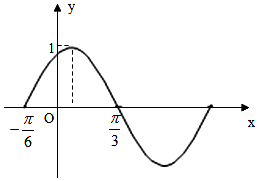 已知函数f(x)=Asin(ωx+ϕ)(其中A>0,|ϕ|<$\frac{π}{2}$,ω>0)的图象如图所示,
已知函数f(x)=Asin(ωx+ϕ)(其中A>0,|ϕ|<$\frac{π}{2}$,ω>0)的图象如图所示, 已知A(-3,0),B(3,0),动点P满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,如图所示作PD⊥x轴,且$\overrightarrow{DM}$=λ$\overrightarrow{DP}$(0<λ<1)
已知A(-3,0),B(3,0),动点P满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,如图所示作PD⊥x轴,且$\overrightarrow{DM}$=λ$\overrightarrow{DP}$(0<λ<1)