题目内容
16.已知向量$\overrightarrow{a}$=(m,1),$\overrightarrow{b}$=(1-n,2),若$\overrightarrow{a}∥\overrightarrow{b}$,则2m+n=1.分析 根据题意,由向量平行的坐标表示公式可得若$\overrightarrow{a}∥\overrightarrow{b}$,则有2×m=1×(1-n),变形可得2m+n=1;即可得答案.
解答 解:根据题意,向量$\overrightarrow{a}$=(m,1),$\overrightarrow{b}$=(1-n,2),
若$\overrightarrow{a}∥\overrightarrow{b}$,则有2×m=1×(1-n),即2m=1-n,
变形可得2m+n=1;
故答案为:1.
点评 本题考查向量平行的坐标运算,关键掌握向量平行的坐标表示公式.

练习册系列答案
相关题目
1.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>b>0)$左右焦点分别为F1,F2,过F1做直线l与双曲线左右分别交于P,Q两点,若三角形PQF2是以Q为直角的等腰直角三角形,则e2=( )
| A. | $5-2\sqrt{2}$ | B. | $5+2\sqrt{2}$ | C. | $4+2\sqrt{2}$ | D. | $4-2\sqrt{2}$ |
5.已知全集U={1,2,3,4,5,6},集合P={1,3,5},Q={1,2,4},则(∁UP)∩Q=( )
| A. | {1} | B. | {2,4} | C. | {2,4,6} | D. | {1,2,4,6} |
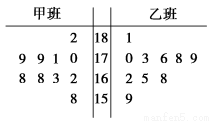
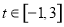 ,则输出的s属于( )
,则输出的s属于( )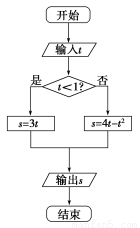
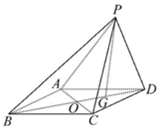 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.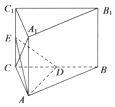 已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.
已知三棱柱ABC-A1B1C1的底面是边长为4的正三角形,侧棱AA1垂直于底面ABC,AA1=2$\sqrt{2}$,D为BC中点.