题目内容
8.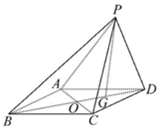 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.
分析 利用向量的三角形法则、平行四边形法则即可得出.
解答 解:$\overrightarrow{PG}$=$\overrightarrow{PB}$+$\overrightarrow{BG}$=$\overrightarrow{PB}$+$\frac{2}{3}$$\overrightarrow{BD}$=$\overrightarrow{PB}$+$\frac{2}{3}$($\overrightarrow{BA}$+$\overrightarrow{BC}$)=$\overrightarrow{PB}$+$\frac{2}{3}$($\overrightarrow{PA}$-$\overrightarrow{PB}$+$\overrightarrow{PC}$-$\overrightarrow{PB}$)=$\frac{2}{3}$$\overrightarrow{PA}$-$\frac{1}{3}$$\overrightarrow{PB}$+$\frac{2}{3}$$\overrightarrow{PC}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$,
而$\overrightarrow{PB}$=$\overrightarrow{PG}$+$\overrightarrow{GB}$,
故$\overrightarrow{BG}$=$\overrightarrow{PG}$-$\overrightarrow{PB}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$-$\overrightarrow{b}$=$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$,
故答案为:$\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$.
点评 本题考查了向量的三角形法则、平行四边形法则及其运算性质,考查了推理能力与计算能力,属于中档题.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案| A. | 当a<0时,f(x)有两个零点 | B. | 当a=0时,f(x)无零点 | ||
| C. | 当0<a<1时,f(x)有小于1的零点 | D. | 当a>1时,f(x)有大于a的零点 |
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
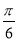 )的图象,可以将函数y=cos 2x的图象 ( )
)的图象,可以将函数y=cos 2x的图象 ( )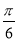 个单位长度
个单位长度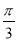 个单位长度
个单位长度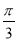 个单位长度
个单位长度