题目内容
6.已知P,Q是圆心在坐标原点O的单位圆上的两点,且分别位于第一象限和第四象限,点P的横坐标为$\frac{4}{5}$,点Q的横坐标为$\frac{5}{13}$,则cos∠POQ=-$\frac{16}{65}$.分析 由条件利用直角三角形中的边角关系求得sin∠xOP和cos∠xOQ的值,利用同角三角函数的基本关系求得cos∠xOP 和 sin∠xOQ,再利用两角和的余弦公式求得cos∠POQ=cos(∠xOP+∠xOQ )的值.
解答 解:由题意可得,cos∠xOP=$\frac{4}{5}$,∴sin∠xOP=$\frac{3}{5}$;
再根据cos∠xOQ=$\frac{5}{13}$,可得sin∠xOQ=$\frac{12}{13}$.
∴cos∠POQ=cos(∠xOP+∠xOQ)=cos∠xOP•cos∠xOQ-sin∠xOP•sin∠xOQ=$\frac{4}{5}×\frac{5}{13}$-$\frac{3}{5}×\frac{12}{13}$=-$\frac{16}{65}$.
故答案为:-$\frac{16}{65}$.
点评 本题主要考查直角三角形中的边角关系,同角三角函数的基本关系,两角和的余弦公式的应用,属于基础题.

练习册系列答案
相关题目
16.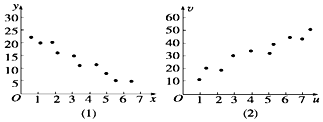 对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )
对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )
 对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )
对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);对变量u,v,有观测数据(ui,vi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )| A. | 变量x与y正相关,u与v正相关 | B. | 变量x与y正相关,u与v负相关 | ||
| C. | 变量x与y负相关,u与v正相关 | D. | 变量x与y负相关,u与v负相关 |
14.设i是虚数单位,复数i(1+ai)为纯虚数,则实数a为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
1.若变量x,y满足的约束条件是$\left\{\begin{array}{l}y≤x\\ x+y≤4\\ y≥k\end{array}\right.$,且z=2x+y的最小值为-6,则k=( )
| A. | 0 | B. | -2 | C. | 2 | D. | 14 |
18.已知圆C:(x-3)2+(y-4)2=1和两点A(-m,0),B(m,0)(m>0).若圆上存在点P使得$\overrightarrow{PA}•\overrightarrow{PB}=0$,则m的取值范围是( )
| A. | (-∞,4] | B. | (6,+∞) | C. | (4,6) | D. | [4,6] |
15.已知直线l:y=k(x+$\sqrt{3}$)和圆C:x2+(y-1)2=1,若直线l与圆C相切,则k=( )
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$或0 | D. | $\sqrt{3}$或0 |