题目内容
20.已知函数f(x)=x2+$\frac{a}{x}$,则“0<a<2”是“函数f(x)在(1,+∞)上为增函数”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 求出函数的导数,问题转化为2x3≥a在区间(1,+∞)上恒成立,求出a的范围,结合集合的包含关系判断即可.
解答 解:f′(x)=2x-$\frac{a}{{x}^{2}}$≥0,
即2x3≥a在区间(1,+∞)上恒成立,
则a≤2,
而0<a<2⇒a≤2,
故选:A.
点评 本题考查了充分必要条件,考查集合的包含关系,是一道基础题.

练习册系列答案
相关题目
10.复数$\frac{3+i}{1-i}$(i为虚数单位)的虚部为( )
| A. | 2i | B. | 2 | C. | -2i | D. | -1 |
11.《九章算术•均输》中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5 钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,乙所得为( )
| A. | $\frac{4}{3}$钱 | B. | $\frac{7}{6}$钱 | C. | $\frac{6}{5}$钱 | D. | $\frac{5}{4}$钱 |
12.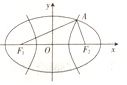 如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
 如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图F1,F2是双曲线${C_1}:{x^2}-\frac{y^2}{8}=1$与椭圆C2的公共焦点,点A是C1,C2在第一象限内的公共点,若|F1F2|=|F1A|,则C2的离心率是( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
9.已知函数f(x)是定义在R上的奇函数,当x≥0时,$f(x)=\frac{1}{2}(|x-1|+|x-2|-3)$,若?x∈R,f(x-a)≤f(x),则a的取值范围是( )
| A. | a≥3 | B. | -3≤a≤3 | C. | a≥6 | D. | -6≤a≤6 |
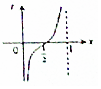
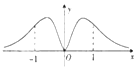
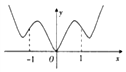
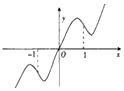
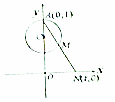 把周长为1的圆的圆心C放在y轴,顶点A(0,1),一动点M从A开始顺时针绕圆运动一周,记走过的弧长$\widehat{AM}$=x,直线AM与x轴交于点N(t,0),则函数t=f(x)的大致图象( )
把周长为1的圆的圆心C放在y轴,顶点A(0,1),一动点M从A开始顺时针绕圆运动一周,记走过的弧长$\widehat{AM}$=x,直线AM与x轴交于点N(t,0),则函数t=f(x)的大致图象( )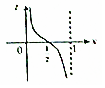


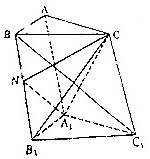 如图,在直三棱柱ABC-A1B1 C1中,AC=2$\sqrt{2}$,AB=BC=BB1=2,N是BB1的中点.
如图,在直三棱柱ABC-A1B1 C1中,AC=2$\sqrt{2}$,AB=BC=BB1=2,N是BB1的中点.