题目内容
10.复数$\frac{3+i}{1-i}$(i为虚数单位)的虚部为( )| A. | 2i | B. | 2 | C. | -2i | D. | -1 |
分析 直接利用复数代数形式的乘除运算化简得答案.
解答 解:∵$\frac{3+i}{1-i}$=$\frac{(3+i)(1+i)}{(1-i)(1+i)}=\frac{2+4i}{2}=1+2i$,
∴复数$\frac{3+i}{1-i}$的虚部为2.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列命题中真命题是( )
| A. | $?x∈({-∞,\frac{π}{4}}),tanx≤1$ | |
| B. | 设l,m表示不同的直线,α表示平面,若m∥l且m⊥α,则l∥α | |
| C. | 利用计算机产生0和l之间的均匀随机数m,则事件“3m-1≥0”发生的概率为$\frac{1}{3}$ | |
| D. | “a>0,b>0”是“$\frac{b}{a}+\frac{a}{b}$≥2”的充分不必要条件 |
19.《九章算术•均输》中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5 钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列,问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,乙所得为( )
| A. | $\frac{4}{3}$钱 | B. | $\frac{5}{4}$钱 | C. | $\frac{6}{5}$钱 | D. | $\frac{7}{6}$钱 |
20.已知函数f(x)=x2+$\frac{a}{x}$,则“0<a<2”是“函数f(x)在(1,+∞)上为增函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
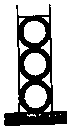 圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.
圆柱形容器内盛有高度为6cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是3cm.